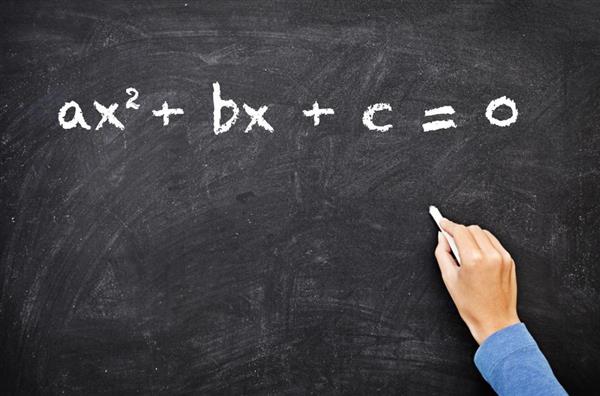Існують кілька способів розв’язування квадратних рівнянь, однак використання формули, яка пов’язує коефіцієнти рівностей названого типу, є універсальним. Цей спосіб часто називають методом “через дискриминант”. Приклади розв’язання квадратних рівнянь з допомогою нього наводяться в даній статті. Про них має знати кожен старшокласник.
Квадратні рівняння
Приклади з дискриминантом ставляться до вирішення квадратних рівнянь. Такі рівняння мають вигляд, представлений на фото нижче.
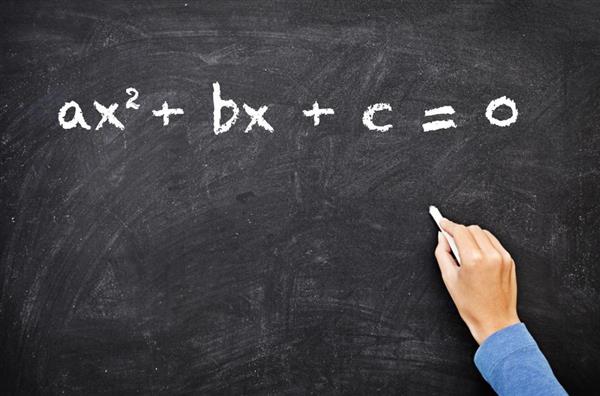
Тут a, b і c – деякі коефіцієнти (числа), які називаються квадратичним, лінійним і вільним членом, відповідно. Якщо відомі значення ікса такі, при яких рівність на фото є істиною, тоді говорять про те, що вони є коренями цього рівняння.
Як можна помітити, це рівняння називається квадратним, бо “2” є максимальним ступенем, до якої зводиться x. Якщо a = 0, тоді рівняння перетворюється в лінійне.
Оскільки максимальна ступінь рівняння дорівнює двом, то можуть існувати лише 0, 1 або 2 його кореня, які будуть приймати дійсні числові значення.
Щоб вирішити назване рівняння, можна скористатися кількома методами. Тим не менш, самим простим і надійним з них є застосування формули з дискриминантом.