Коли розглядають рух тіл у вільному просторі, будь то переміщення планет в космосі чи об’єктів в земній атмосфері, то визначальними траєкторію силами є гравітаційні. У даній статті розглядається один із видів такого переміщення – рух під кутом до горизонту. Формули, необхідні для розв’язання відповідних завдань, також наводяться.
Про якому типі руху піде мова?
Рух під кутом до горизонту (формули наведені далі в статті) – це переміщення об’єктів у гравітаційному полі нашої планети, в процесі якого діє лише одна-єдина сила – сила тяжіння. Насправді ж присутня ще опір повітря, але їм прийнято нехтувати.
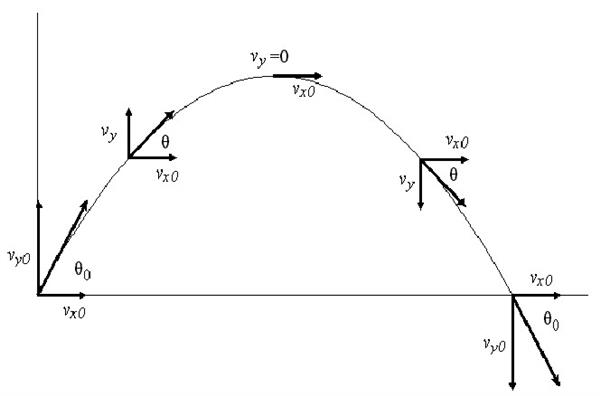
У процесі руху під кутом до горизонту тіло починає рух або з поверхні землі або з деякої висоти h. У початковий момент часу воно має швидкість v, спрямованої під деяким кутом до горизонту. Пролетівши по деякій траєкторії, тіло падає на землю.
Зазначену траєкторію прийнято вважати параболічної, проте це не зовсім вірно. Справа в тому, що в результаті дії сили тяжіння об’єкт рухається по еліптичній траєкторії (через падіння на землю тіло описує лише частину еліпса). У ряді випадків частину реальної еліптичної траєкторії можна представити у вигляді параболи з високою точністю, що і робиться з метою спростити математичні викладки при розрахунках.