Вектор є важливим геометричним об’єктом, за допомогою властивостей якого зручно вирішувати багато проблем на площині і в просторі. У цій статті дамо йому визначення, розглянемо його основні характеристики, а також покажемо, як для задання площин вектор у просторі може бути використаний.
Що таке вектор: двовимірний випадок
У першу чергу необхідно чітко розуміти, про який об’єкт йде мова. В геометрії вектором називається спрямований відрізок. Як і будь-який відрізок, він характеризується двома основними елементами: початкової і кінцевої точок. Координати цих точок однозначно визначають всі характеристики вектора.
Розглянемо приклад вектора на площині. Для цього проведемо дві взаємно перпендикулярні осі x і y. Зазначимо довільну точку P(x, y). Якщо поєднати цю точку з початком координат (точка O), а потім вказати напрямок до P, тоді ми отримаємо вектор OP (далі в статті риска над символом показує, що розглядається вектор). Малюнок вектора на площині зображено нижче.
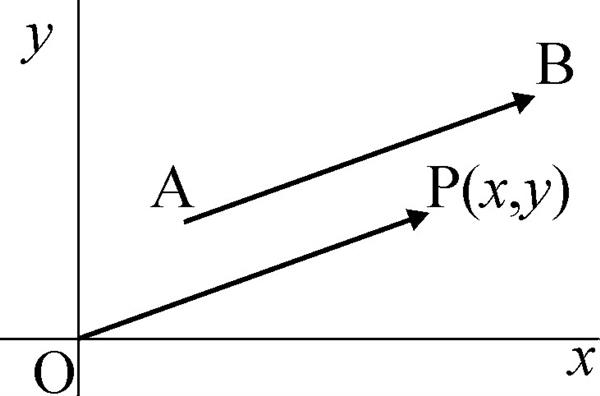
Тут також зображено інший вектор AB, і видно, що його характеристики абсолютно ідентичні OP, однак він знаходиться в іншій частині системи координат. Шляхом паралельного перенесення OP можна отримати нескінченну кількість векторів з однаковими властивостями.

