У фізиці розгляд завдань з обертовими тілами або системами, які знаходяться в рівновазі, здійснюється з використанням концепції “момент сили”. У цій статті буде розглянута формула моменту сили, а також її використання для вирішення певного типу завдань.
Момент сили у фізиці
Як було зазначено у вступі, в даній статті піде мова про системи, які можуть обертатися або навколо осі, або навколо точки. Розглянемо приклад такої моделі, зображеної на малюнку нижче.
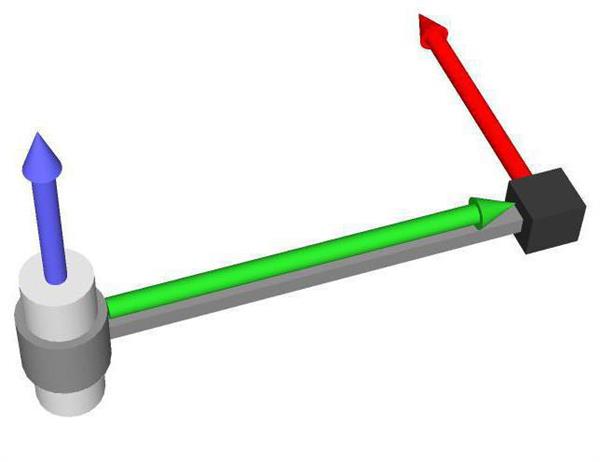
Ми бачимо, що важіль сірого кольору закріплений на осі обертання. На кінці важеля є чорний кубик деякої маси, на який діє сила (червона стрілка). Інтуїтивно зрозуміло, що результатом впливу цієї сили буде обертання важеля навколо осі проти годинникової стрілки.
Моментом сили називається величина у фізиці, яка дорівнює векторному добутку радіуса, що з’єднує вісь обертання і точку прикладання сили (зелений вектор на малюнку), і самій зовнішній силі. Тобто формула моменту сили відносно осі записується наступним чином:
M = r * F
Результатом цього твору буде вектор M. Напрямок його визначають, виходячи зі знання векторів-множників, тобто r і F. Згідно з означенням векторного добутку, M повинен бути перпендикулярний площині, утвореної векторами r і F, і спрямований у відповідності з правилом правої руки (якщо чотири пальці правої руки розташувати вздовж першого умножаемого вектора в напрямку до кінця другого, то відставлений вгору великий палець вкаже, куди спрямований шуканий вектор). На малюнку можна бачити, куди спрямований вектор M (синя стрілка).

