Пряма разом з точкою є важливими елементами геометрії, з допомогою яких будуються багато фігури у просторі і на площині. У цій статті докладно розглядається параметричне рівняння прямої, а також його зв’язок з іншими типами рівнянь для цього геометричного елемента.
Пряма і рівняння для її опису
Пряма в геометрії являє собою сукупність точок, які з’єднують довільні дві точки простору відрізком з найменшою довжиною. Цей відрізок є частиною прямої. Будь-які інші криві, що з’єднують зафіксовані дві точки в просторі, будуть мати більшу довжину, тому не є прямими.
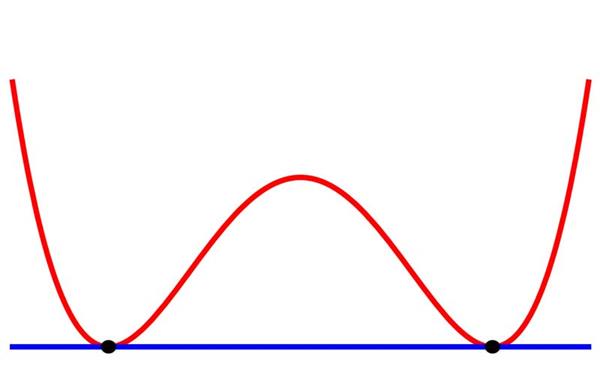
На малюнку вище показано дві чорні точки. Синя лінія, що з’єднує їх, є прямою, а червона – кривий. Очевидно, що довжина червоної лінії між чорними крапками більше, ніж синій.
Існують кілька видів рівнянь прямої, з допомогою яких можна описати пряму в тривимірному просторі або в двовимірному. Нижче наведені назви цих рівнянь:
- векторне;
- параметричне;
- у відрізках;
- симетричне або канонічне;
- загального типу.
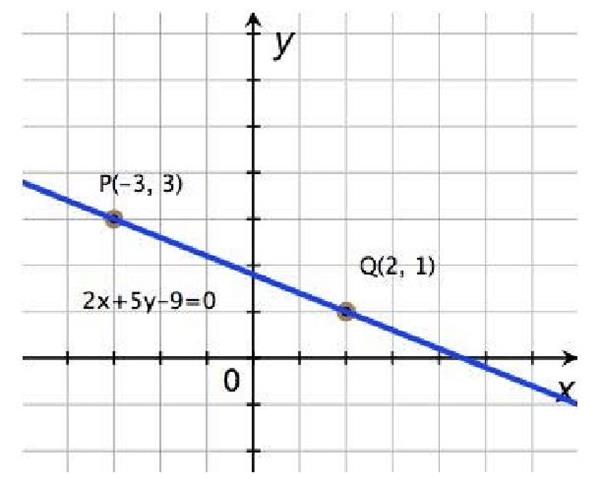
У цій статті розглянемо параметричне рівняння прямої, однак виведемо його з векторного. Також покажемо зв’язок параметричного і симетричного або канонічного рівняння.
Векторне рівняння
Зрозуміло, що всі наведені типи рівнянь для розглянутого геометричного елемента пов’язані між собою. Тим не менш векторне рівняння є базовим для всіх них, оскільки воно безпосередньо випливає з визначення прямої. Розглянемо, як воно вводиться в геометрію.
Припустимо, дана точка в просторі P(x0; y0; z0). Відомо, що ця точка належить прямій. Скільки прямих можна провести через неї? Нескінченна безліч. Тому для того, щоб можна було провести єдину пряму, необхідно задати напрям останньої. Напрямок, як відомо, визначається вектором. Позначимо його v(a; b; c), де символи в дужках – це його координати. Для кожної точки Q(x; y; z), яка знаходиться на даній прямій, можна записати рівність:
(x; y; z) = (x0; y0; z0) + α × (a; b; c)
Тут символ α є параметром, що приймають абсолютно будь-яке дійсне значення (множення вектора на число може змінити тільки його модуль або напрям на протилежне). Ця рівність називається векторним рівнянням для прямої у тривимірному просторі. Змінюючи параметр α, ми отримуємо всі точки (x; y; z), які утворюють цю пряму.
Стоїть в рівнянні вектор v(a; b; c) називається направляючим. Пряма не має конкретного напрямку, а її довжина є нескінченною. Ці факти означають, що будь-який вектор, отриманий з v за допомогою множення на дійсне число, також буде напрямних для прямої.
Що стосується точки P(x0; y0; z0), то замість неї рівняння можна підставити довільну точку, яка лежить на прямій, і остання при цьому не зміниться.
Малюнок вище демонструє пряму (синя лінія), яка задана в просторі через напрямний вектор (червоний спрямований відрізок).
Не представляє ніякої праці отримати таку рівність для двовимірного випадку. Використовуючи аналогічні міркування приходимо до виразу:
(x; y) = (x0; y0) + α × (a; b)
Бачимо, що воно повністю таке ж, як і попередній, тільки використовуються дві координати замість трьох для задання точок і векторів.
Параметричне рівняння
Спочатку отримаємо в просторі параметричне рівняння прямої. Вище, коли записувалося векторне рівність, вже згадувалося про параметр, який в ньому присутній. Щоб отримати параметричне рівняння, достатньо розкрити векторне. Отримуємо:
x = x0 + α × a;
y = y0 + α × b;
z = z0 + α × c
Сукупність цих трьох лінійних рівностей, в кожному з яких є одна змінна координата і параметр α, прийнято називати параметричним рівнянням прямої в просторі. По суті, ми не зробили нічого нового, а просто явно записали зміст відповідного векторного вираження. Відзначимо лише один момент: число α, хоча і є довільним, але воно для всіх трьох рівностей однакове. Наприклад, якщо α = -1,5 для 1-го рівності, то таке ж його значення слід підставити у друге і третє рівності при визначенні координат точки.
Параметричне рівняння прямої на площині подібно такому для просторового випадку. Воно записується у вигляді:
x = x0 + α × a;
y = y0 + α × b
Таким чином, щоб скласти параметричне рівняння прямої, що слід записати в явному вигляді векторне рівняння для неї.
Отримання канонічного рівняння
Як вище було зазначено, всі рівнянь, які задають пряму у просторі і на площині, виходять одне з одного. Покажемо, як отримати з параметричного канонічне рівняння прямої. Для просторового випадку маємо:
x = x0 + α × a;
y = y0 + α × b;
z = z0 + α × c
Виразимо параметр в кожному рівність:
α = (x – x0) / a;
α = (y – y0) / b;
α = (z – z0) / c
Оскільки ліві частини є однаковими, тоді праві частини рівностей теж дорівнюють один одному:
(x – x0) / a = (y – y0) / b = (z – z0) / c
Це і є канонічне рівняння прямої в просторі. Значення знаменника у кожному виразі є відповідною координатою направляючого вектора. Значення в чисельнику, які віднімаються з кожної змінної, представляють собою координати точки, яка належить цій прямій.
Відповідне рівняння для випадку на площині прийме вигляд:
(x – x0) / a = (y – y0) / b
Далі в статті вирішимо кілька завдань, використовуючи отримані знання.
Рівняння прямої через 2 точки
Відомо, що дві фіксовані точки як на площині, так і в просторі однозначно задають пряму. Припустимо, що задані дві наступні точки на площині:
P(x1; y1);
Q(x2; y2)
Як скласти рівняння прямої через них? Для початку слід визначити напрямний вектор. Його координати мають наступні значення:
PQ(x2 – x1; y2 – y1)
Тепер можна записати рівняння в будь-якому з трьох видів, які були розглянуті в пунктах вище. Наприклад, параметричне рівняння прямої приймає вигляд:
x = x1 + α × (x2 – x1);
y = y1 + α × (y2 – y1)
В канонічній формі можна переписати так:
(x – x1 ) / (x2 – x1) = (y – y1) / (y2 – y1)
Видно, що у канонічне рівняння входять координати обох точок, причому в чисельнику можна змінювати ці точки. Так, останнє рівняння можна переписати наступним чином:
(x – x2) / (x2 – x1) = (y – y2) / (y2 – y1)
Всі записані вирази називаються рівняннями прямої через 2 точки.
Завдання з трьома точками
Дано координати трьох точок:
M (5; 3; -1);
N (2; 2; 0);
K (1; -1; -5)
Необхідно визначити, ці точки лежать на одній прямій чи ні.
Вирішувати цю задачу так: спочатку скласти рівняння прямої для будь-яких двох точок, а потім підставити в нього координати третьої і перевірити, чи задовольняють вони отриманого рівності.
Складаємо рівняння через M і N в параметричній формі. Для цього застосуємо отриману в пункті вище формулу, яку узагальнимо на тривимірний випадок. Маємо:
x = 5 + α × (-3);
y = 3 + α × (-1);
z = -1 + α × 1
Тепер підставимо ці вирази координати точки K і знайдемо значення параметра альфа, який їм відповідає. Отримуємо:
1 = 5 + α × (-3) => α = 4/3;
-1 = 3 + α × (-1) => α = 4;
-5 = -1 + α × 1 => α = -4
Ми з’ясували, що всі три рівності справедливі, якщо кожне з них візьме відрізняється від інших значення параметра α. Останній факт суперечить умові параметричного рівняння прямої, в якому α повинні бути рівними для всіх рівнянь. Це означає, що точка K прямої MN не належить, а значить, всі три точки на одній прямій не лежать.
Завдання на паралельність прямих
Дано два рівняння прямих у параметричному вигляді. Вони представлені нижче:
x = -1 + 5 × α;
y = 3 + 3 × α
і
x = 2 – 6 × λ;
y = 4 – 3,6 × λ
Необхідно визначити, чи є прямі паралельними. Найпростіше визначити паралельність двох прямих з використанням координат направляючих векторів. Звертаючись до загальної формулою параметричного рівняння в двовимірному просторі, отримуємо, що направляючі вектори кожної прямий матимуть координати:
v1(5; 3);
v2(-6; -3,6)
Два вектора є паралельними, якщо один з них можна отримати шляхом множення іншого на деяке число. Розділимо попарно координати векторів, одержимо:
-6/5 = -1,2;
-3,6/3 = -1,2
Це означає що:
v2 = -1,2 × v1
Направляючі вектори v2 і v1 паралельні, значить, прямі в умові задачі теж є паралельними.
Перевіримо, чи не є вони одній і тій же прямій. Для цього потрібно підставити координати будь-якої точки в рівняння для іншої. Візьмемо точку (-1; 3), підставимо її в рівняння для другої прямої:
-1 = 2 – 6 × λ => λ = 1/2;
3 = 4 – 3,6 × λ => λ ≈ 0,28
Тобто прямі є різними.
Завдання на перпендикулярність прямих
Дано рівняння двох прямих:
x = 2 × α;
y = 1 + 3 × α
і
x = 2 + 6 × λ;
y = -2 – 4 × λ
Перпендикулярні ці прямі?
Дві прямі будуть перпендикулярні, якщо скалярний добуток їх направляючих векторів дорівнює нулю. Випишемо ці вектора:
v1(2; 3);
v2(6; -4)
Знайдемо їх скалярний добуток:
(v1 × v2) = 2 × 6 + 3 × (-4) = 12 – 12 = 0
Таким чином, ми з’ясували, що розглянуті прямі перпендикулярні. Вони зображені на малюнку вище.
