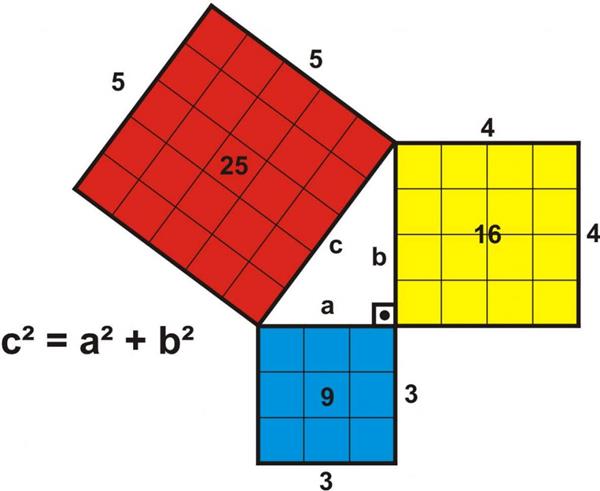
Кожен школяр знає, що завжди квадрат гіпотенузи дорівнює сумі катетів, кожен з яких зведений у квадрат. Ця твердження носить назву теореми Піфагора. Вона є однією з найбільш відомих теорем тригонометрії і математики в цілому. Розглянемо її детальніше.
Поняття про прямокутному трикутнику
Перед тим, як переходити до розгляду теореми Піфагора, в якій квадрат гіпотенузи дорівнює сумі катетів, які зведені в квадрат, слід розглянути поняття і властивості прямокутного трикутника, для якого справедлива теорема.
Трикутник – плоска фігура, що має три кути і три сторони. Прямокутний ж трикутник, як випливає з його назви, має один прямий кут, тобто цей кут дорівнює 90 o.
З загальних властивостей всіх трикутників відомо, що сума всіх трьох кутів цієї фігури дорівнює 180 o, а це означає, що для прямокутного трикутника сума двох кутів, які не є прямими, становить 180 o – 90 o = 90o. Останній факт означає, що будь-який кут в прямокутному трикутнику, який не є прямим, буде завжди менше 90o.
Сторону, яка лежить проти прямого кута, прийнято називати гіпотенузою. Дві ж інші сторони є катетами трикутника, вони можуть бути рівні між собою, а можуть і відрізнятися. З тригонометрії відомо, що чим більше кут, проти якого лежить сторона в трикутнику, тим більше довжина цієї сторони. Це означає, що в прямокутному трикутнику гіпотенуза (лежить проти кута 90 o) буде завжди більше будь-якого з катетів (лежать проти кутів < 90o).