При вивченні стереометрії однією з головних тем стає «Циліндр». Площа бічної поверхні вважається якщо не головною, то важливою формулою при рішенні геометричних задач. Однак важливо пам’ятати і визначення, які допоможуть зорієнтуватися в прикладах і при доведення різних теорем.
Поняття циліндра
Спочатку потрібно розглянути кілька визначень. Тільки після їх вивчення можна приступати до розгляду питання про формулу площі бічної поверхні циліндра. На основі цього запису можна обчислити і інші вирази.
- Під циліндричною поверхнею розуміють площину, описувану твірної, що рухається і залишається паралельної заданому напрямку, ковзної за наявною кривої.
- Є і друге визначення: циліндричну поверхню утворюють безліч паралельних прямих, які перетинають задану криву.
- Утворює називають умовно висоту циліндра. При її переміщенні навколо осі, що проходить через центр основи, виходить позначене геометричне тіло.
- Під віссю передбачають пряму, що проходить через обидва підстави фігури.
- Циліндром називається стереометрическое тіло, обмежене пересічними бічною поверхнею і 2 паралельними площинами.
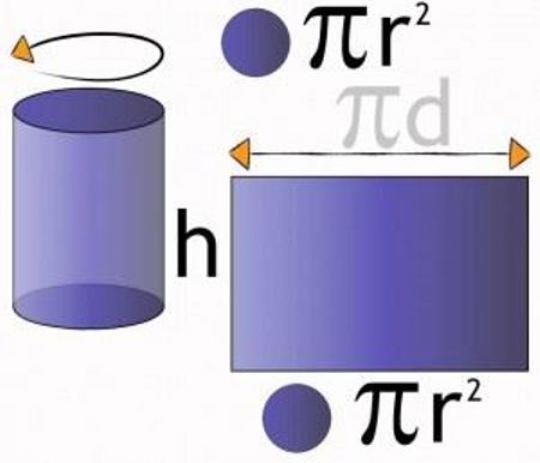
Існують різновиди цієї об’ємної фігури:
- Під круговим увазі циліндр, напрямна якого – це коло. Його головними складовими вважаються радіус основи і утворює. Остання дорівнює висоті фігури.
- Існує прямий циліндр. Свою назву він отримав завдяки перпендикулярності твірної до підстав фігури.
- Третій вид – скошений циліндр. У підручниках можна зустріти й інша його назва «круговий циліндр зі скошеним підставою». Дану фігуру визначає радіус основи, мінімальна і максимальна висоти.
- Під рівностороннім циліндром розуміють тіло, що має рівні між собою висоту і діаметр круглої площині.

