Ще в Стародавньому Єгипті з’явилася наука, за допомогою якої можна було вимірювати об’єми, площі та інші величини. Поштовхом до цього послужило будівництво пірамід. Воно передбачало значне число складних розрахунків. І крім будівництва, було важливо правильно виміряти землю. Звідси і з’явилася наука “геометрія” від грецьких слів “геос” – земля і “метрио” – вимірюю.
Дослідження геометричних форм сприяло спостереження астрономічних явищ. І вже в 17-м столітті до н.е. були знайдені початкові способи розрахунку площі кола, об’єму кулі та найголовніше відкриття – теорема Піфагора.
Формулювання теореми про кола, вписаного в трикутник виглядає наступним чином:
У трикутник можна вписати тільки одну окружність.
При такому розташуванні окружність – вписана, а трикутник – описаний навколо кола.
Формулювання теореми про центр кола, вписаного в трикутник, виглядає наступним чином:
Центральна точка кола, вписаного у трикутник, є точка перетину бісектрис трикутника.
Коло, вписане в рівнобедрений трикутник
Окружність вважається вписаного в трикутник, якщо вона хоча б однією точкою стосується всіх його сторін.
На фото нижче показана окружність, що знаходиться всередині рівнобедреного трикутника. Умова теореми про кола, вписаного в трикутник, дотримано – вона стосується всіх сторін трикутника АВ, ВС І СА в точках R, S, Q відповідно.
Одним із властивостей рівнобедреного трикутника є те, що вписана окружність точкою дотику ділить основу навпіл (BS = SC), а радіус вписаного кола становить третину висоти даного трикутника(SP=AS/3).
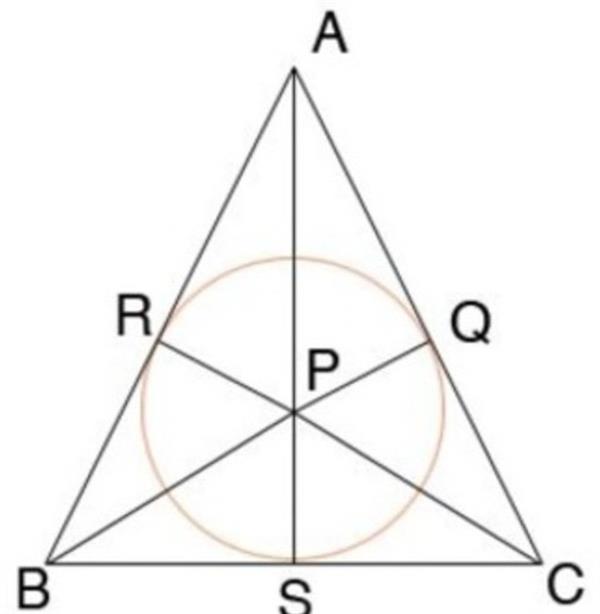
Властивості теореми про кола, вписаного в трикутник:
- Відрізки, що виходять з однієї вершини трикутника до точок дотику з окружністю, рівні. На малюнку AR = AQ, BR = BS, CS = CQ.
- Радіус кола (вписаною) – це площа, поділена на півпериметр трикутника. Як приклад, потрібно накреслити рівнобедрений трикутник з тими ж буквеними позначеннями, що на картинці, наступних розмірів: основа ВС = 3 см, висота AS = 2 см, сторони АВ=ВС, відповідно, виходять за 2,5 см кожна. Проведемо з кожного кута биссектрису і місце їх перетину позначимо як Р. Впишемо окружність з радіусом PS, довжину якого потрібно знайти. Дізнатися площа трикутника можна, помноживши 1/2 основи на висоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Півпериметр трикутника дорівнює 1/2 суми всіх сторін: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, що повністю відповідає дійсності, якщо виміряти лінійкою. Відповідно, вірно теореми про властивість кола, вписаного в трикутник.
Коло, вписане в прямокутний трикутник
Для трикутника з прямим кутом діють властивості теореми про вписаного в трикутник кола. І, крім того, додається можливість вирішувати завдання з постулатами теореми Піфагора.

Радіус вписаного кола в прямокутний трикутник можна визначити наступним чином: скласти довжини катетів, відняти значення гіпотенузи і вийшло значення розділити на 2.
Є хороша формула, яка допоможе вирахувати площу трикутника – периметр помножити на радіус вписаного в цей трикутник кола.
Формулювання теореми про вписаного кола
У планіметрії важливі теореми про вписаних і описаних фігурах. Одна з них звучить так:
Центр кола, вписаного у трикутник, є точкою перетину бісектрис, проведених з його кутів.

На представленому малюнку показано доказ цієї теореми. Показано рівність кутів, і, відповідно, рівність прилеглих трикутників.
Теорема про центр кола, вписаного в трикутник
Радіуси кола, вписаного в трикутник, проведені в точки дотику перпендикулярні сторонам трикутника.
Завдання «сформулюйте теорему про кола вписаного у трикутник» не має застати зненацька, тому що це одні з фундаментальних і найпростіших знань в геометрії, якими необхідно володіти повною мірою для вирішення багатьох практичних завдань у реальному житті.

