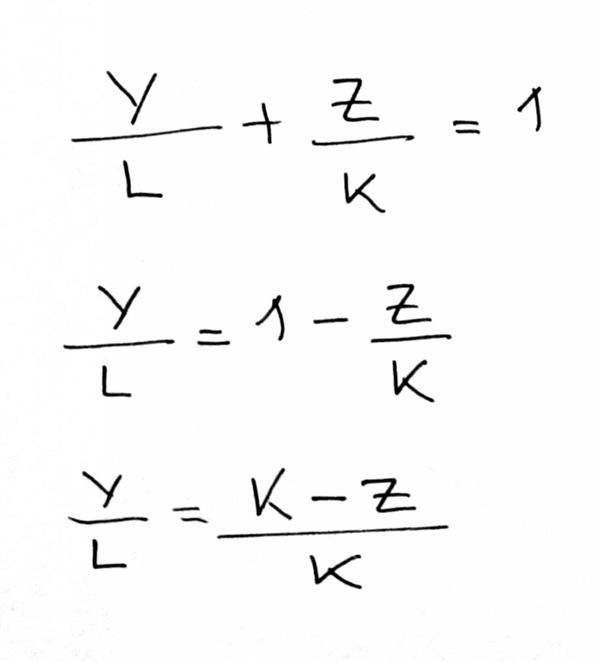Для визначення паралельності та перпендикулярності площин, а також для розрахунку відстаней між цими геометричними об’єктами, зручно користуватися тим чи іншим видом числових функцій. Для яких завдань зручно використовувати рівняння площини у відрізках? У цій статті розглянемо, що це і як використовувати в практичних завданнях.
Що являє собою рівняння у відрізках?
Площину можна задати в тривимірному просторі кількома способами. У цій статті деякі з них будуть наведені під час розв’язування задач різного типу. Тут же дамо детальну характеристику рівняння площини у відрізках. Воно в загальному випадку має наступний вигляд:
x/p + y/q + z/r = 1.
Де символами p, q, r позначені деякі конкретні числа. Це рівняння можна легко перевести у вираз загального виду та інші форми числових функцій для площини.
Зручність запису рівняння у відрізках полягає в тому, що воно містить явні координати перетину площини з перпендикулярними осями координат. На осі x відносно початку координат площину відсікає відрізок завдовжки p, y дорівнює q, z – довжиною r.
Якщо який-небудь з трьох змінних не міститься в рівнянні, то це означає, що через відповідну вісь площину не проходить (математики кажуть, що перетинає в нескінченності).
Далі наведемо кілька завдань, в яких покажемо, як працювати з цим рівнянням.
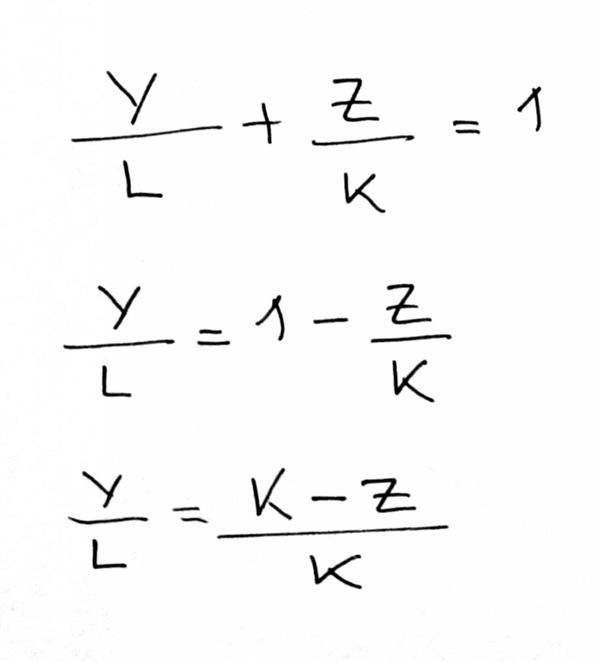
Зв’язок загального і у відрізках рівнянь
Відомо, що площина задана наступним рівністю:
2*x – 3*y + z – 6 = 0.
Необхідно це загальне рівняння площини у відрізках записати.
Коли виникає подібна задача, потрібно дотримуватися такої методики: переносимо вільний член в праву частину рівності. Потім ділимо на цей член все рівняння, прагнучи його виразити у вигляді, наведеному в попередньому пункті. Маємо:
2*x – 3*y + z = 6 =>
2*x/6 – 3*y/6 + z/6 = 1 =>
x/3 + y/(-2) + z/6 = 1.
Ми отримали у відрізках рівняння площини, заданий спочатку в загальному вигляді. Помітно, що площина відтинає відрізки з довжинами 3, 2 і 6 для осей x, y і z відповідно. Вісь y площина перетинає в негативній області координат.
При складанні рівняння у відрізках важливо, щоб перед усіма змінними стояв знак “+”. Тільки в цьому випадку число, на яке ця змінна ділиться, покаже отсекаемую на осі координату.
Нормальний вектор і точка на площині
Відомо, що деяка площина має напрямний вектор (3; 0; -1). Також відомо, що вона проходить через точку (1; 1; 1). Слід для цієї площини написати рівняння у відрізках.
Щоб вирішити цю задачу, слід для початку скористатися загальною формою для цього двовимірного геометричного об’єкта. Загальна форма записується у вигляді:
A*x + B*y + C*z + D = 0.
Три перших коефіцієнта є тут координатами вектора направляючого, який задано в умові задачі, тобто:
A = 3;
B = 0;
C = -1.
Залишається знайти вільний член D. Його можна визначити за такою формулою:
D = -1*(A*x1 + B*y1 + C*z1).
Де значення координат з індексом 1 відповідають координатам точки, що належить площині. Підставляємо їх значення з умови задачі, отримуємо:
D = -1*(3*1 + 0*1 + (-1)*1) = -2.
Тепер можна записати повністю рівняння:
3*x – z – 2 = 0.
Вище вже була продемонстрована методика перетворення цього виразу в рівняння площини у відрізках. Застосуємо її:
3*x – z = 2 =>
x/(2/3) + z/(-2) = 1.
Відповідь на завдання отримано. Зауважимо, що дана площина перетинає тільки x і z осі. Для y вона паралельна.
Дві прямі, що задають площину
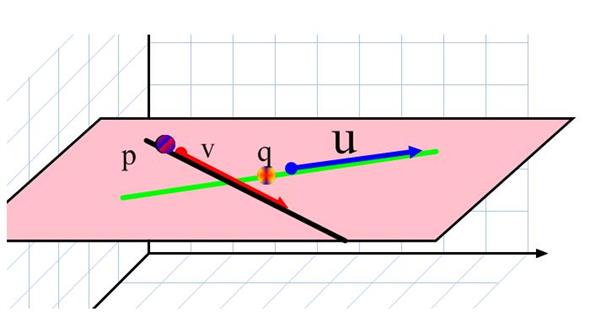
З курсу просторової геометрії кожен школяр знає, що дві довільні прямі однозначно задають площину в тривимірному просторі. Розв’яжемо таку задачу.
Відомі два рівняння прямих:
(x; y; z) = (1; 0; 0) + α*(2; -1; 0);
(x; y; z) = (1; -1; 0) + β*(-1; 0; 1).
Потрібно записати у відрізках рівняння площини, через ці прямі проходить.
Так як обидві прямі повинні лежати в площині, то це означає, що їх вектора (напрямні) повинні бути перпендикулярні вектору (спрямовує) для площини. У той же час відомо, що векторний добуток довільних двох спрямованих відрізків дає результат у вигляді координат третього, перпендикулярного двом вихідним. Враховуючи цю властивість, отримуємо координати нормального до шуканої площини вектора:
[(2; -1; 0)*(-1; 0; 1)] = (-1; -2; -1).
Оскільки його можна помножити на довільне число, при цьому утворюється новий спрямований відрізок, паралельний, то можна знак отриманих координат замінити на протилежний (помножити на -1), отримаємо:
(1; 2; 1).
Нам відомий напрямний вектор. Залишається взяти довільну точку однієї з прямих і скласти загальне рівняння площини:
A = 1;
B = 2;
C = 1;
D = -1*(1*1 + 2*0 + 3*0) = -1;
x + 2*y + z -1 = 0.
Переводимо це рівність у вираз у відрізках, отримуємо:
x + 2*y + z = 1 =>
x/1 + y/(1/2) + z/1 = 1.
Таким чином, площина перетинає всі три осі в позитивній області координатної системи.
Три точки і площину
Так само як дві прямі, три крапки задають площину однозначно в тривимірному просторі. Запишемо відповідне рівняння у відрізках, якщо відомі наступні координати точок, що лежать у площині:
Q(1;-2;0);
P(2;-3;0);
M(4; 1; 0).
Поступимо таким чином: обчислимо координати двох довільних векторів, що з’єднують ці точки, потім, знайдемо нормальний до площині вектор n, розрахувавши твір знайдених спрямованих відрізків. Отримуємо:
QP = P – Q = (1; -1; 0);
QM = M – Q = (2; 4; 0);
n = [QP*QM] = [(1; -1; 0)*(2; 4; 0)] = (0; 0; 6).
Візьмемо для прикладу точку P, складемо рівняння площини:
A = 0;
B = 0;
C = 6;
D = -1*(0*2 + 0*(-3) + 6*0) = 0;
6*z = 0 або z = 0.
Ми отримали просте вираз, що відповідає площині xy в даній прямокутній системі координат. Записати його у відрізках не можна, оскільки осі x і y належать площині, а довжина отсекаемого на осі z відрізка дорівнює нулю (точка (0; 0; 0) належить площині).