Конус – це одна з просторових фігур обертання, характеристики і властивості яких вивчає стереометрія. У цій статті дамо визначення цієї фігури і розглянемо основні формули, що зв’язують лінійні параметри конуса з його площею поверхні і об’ємом.
Що це – конус?
З точки зору геометрії мова йде про просторової фігури, яка утворена сукупністю прямих відрізків, що з’єднують деяку точку простору з усіма точками плавною плоскої кривої. Цієї кривої може бути коло або еліпс. На малюнку нижче показаний конус.

Представлена фігура не володіє об’ємом, оскільки стінки її поверхні мають нескінченно малу товщину. Однак якщо її заповнити речовиною і обмежити зверху не кривий, а плоскою фігурою, наприклад колом, то ми отримаємо тверде об’ємне тіло, яке також прийнято називати конусом.
Форму конуса можна часто зустріти в житті. Так, нею володіє морозиво-ріжок або смугасті чорно-помаранчеві дорожні конуси, які виставляють на проїзну частину для привертання уваги учасників руху.

Елементи конуса і його види
Оскільки конус полиэдром не є, то кількість утворюючих його елементів не так велика, як для многогранників. В геометрії конус загального виду складається з наступних елементів:
- підстави, що обмежує крива якого називається директрисою, або твірної;
- бічній поверхні, яка є сукупністю всіх точок прямих відрізків (генератрис), що з’єднують вершину і точки напрямної кривої;
- вершини, яка є точкою перетину генератрис.
Зауважимо, що вершина в площині підстави не повинна лежати, оскільки в цьому випадку конус вироджується у плоску фігуру.
Якщо з вершини провести перпендикулярний відрізок до основи, то ми отримаємо висоту фігури. Якщо остання підстава перетинає в геометричному центрі, то це прямий конус. Якщо ж перпендикуляр не збігається з геометричним центром підстави, то фігура буде похилою.
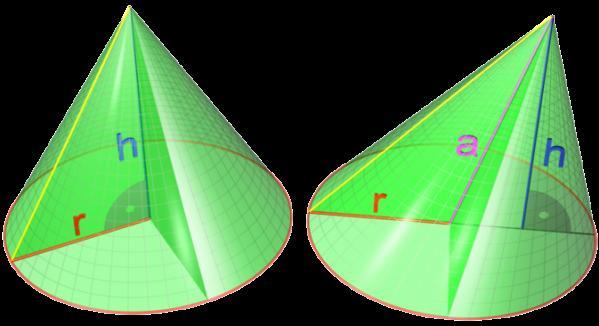
Прямий і похилий конуси показано на рисунку. Тут висота і радіус основи конуса позначені h і r відповідно. Лінія, яка з’єднує вершину фігури і геометричний центр заснування, є віссю конуса. З малюнка видно, що для прямої фігури висота лежить на цій осі, а для похилої висота фігури з віссю утворює деякий кут. Вісь конуса позначена буквою a.
Прямий конус з круглим підставою
Мабуть, це конус найпоширеніший з розглянутого класу фігур. Складається він з кола і бічної поверхні. Отримати геометричними методами його не представляє ніякої праці. Для цього слід взяти прямокутний трикутник і обертати його навколо осі, що збігається з одним з катетів. Очевидно, що цей катет стане висотою фігури, а довжина другого катета трикутника утворює радіус основи конуса. Схема нижче демонструє описану схему отримання даної фігури обертання.
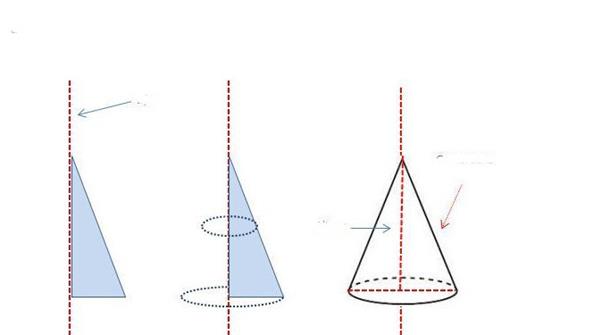
Зображений трикутник можна обертати навколо іншого катета, при цьому вийде конус з великим радіусом підстави і меншою висотою, ніж перший.
Для однозначного визначення всіх параметрів круглого прямого конуса слід знати будь-які дві його лінійних характеристики. Серед них виділяють радіус r, висоту h або довжину генератрисы g. Всі названі величини є довжинами сторін розглянутого прямокутного трикутника, тому для їх зв’язку справедлива теорема Піфагора:
g2 = r2 + h2.
Площа поверхні
При вивченні поверхні будь об’ємної фігури зручно користуватися її розгорткою на площину. Конус не є винятком. Для круглого конуса розгортка показана нижче.
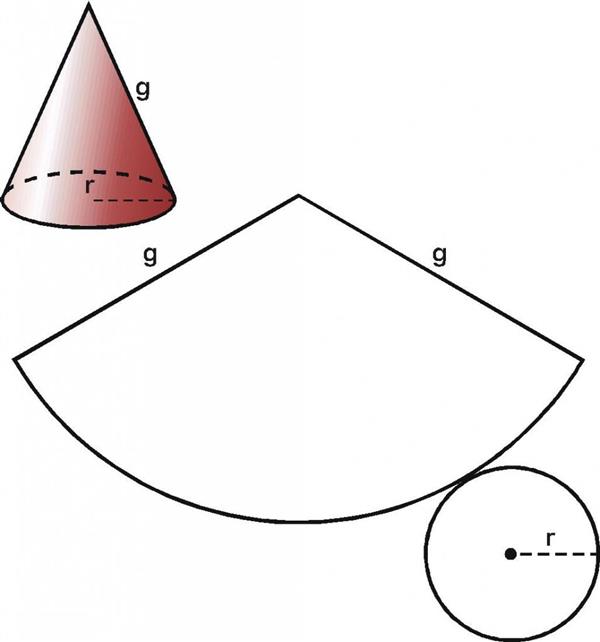
Ми бачимо, що розгортка фігури складається з двох частин:
- Кола, який утворює підставу конуса.
- Сектора кола, що є конічною поверхнею фігури.
Площа круга знайти легко, і відповідна формула відома кожному школяру. Говорячи про круговому секторі, зауважимо, що він є частиною кола з радіусом g (довжина генератрисы конуса). Довжина дуги цього сектора дорівнює довжині кола основи. Ці параметри дозволяють однозначно визначити його площу. Відповідна формула має вигляд:
S = pi*r2 + pi*r*g.
Перше і друге доданки у виразі – це конуса основи і бічної поверхні площі відповідно.
Якщо довжина генератрисы g невідома, але дана висота h фігури, тоді формулу можна переписати у вигляді:
S = pi*r2 + pi*r*√(r2 + h2).
Обсяг фігури
Якщо взяти пряму піраміду і збільшувати на нескінченності число сторін її підстави, то форма підстави буде прагнути до кола, а бічна поверхня піраміди буде наближатися до конічної поверхні. Ці міркування дозволяють використовувати формулу для об’єму піраміди при розрахунку аналогічної величини для конуса. Обсяг конуса може бути знайдений за формулою:
V = 1/3*h*So.
Справедлива ця формула завжди, незалежно від того, що являє собою підставу конуса, що має площу So. Більш того, формула застосовна також для нахиленого конуса.
Оскільки ми вивчаємо властивості прямої фігури з круглим підставою, то для визначення його об’єму можна користуватися таким виразом:
V = 1/3*h*pi*r2.
Справедливість формули очевидна.
Завдання на знаходження площі поверхні та об’єму
Нехай дано конус, радіус якого дорівнює 10 см, а довжина твірної становить 20 див. Необхідно визначити об’єм і площа поверхні для цієї фігури.
Для обчислення площі S можна скористатися формулою, записаної вище. Маємо:
S = pi*r2 + pi*r*g = 942 см2.
Для визначення обсягу необхідно знати висоту h фігури. Розрахуємо її, користуючись зв’язком між лінійними параметрами конуса. Отримуємо:
h = √(g2 – r2) = √(202 – 102) ≈ 17,32 див.
Тепер можна скористатися формулою для V:
V = 1/3*h*pi*r2 = 1/3*17,32*3,14*102 ≈ 1812,83 см3.
Зазначимо, що обсяг круглого конуса становить третю частину від циліндра, в який він вписаний.

