При математичному описі обертального руху важливо знати момент інерції системи відносно осі. В загальному випадку процедура знаходження цієї величини передбачає реалізацію процесу інтегрування. Полегшити обчислення дозволяє так звана теорема Штейнера. Розглянемо її докладніше в статті.
Що таке момент інерції?
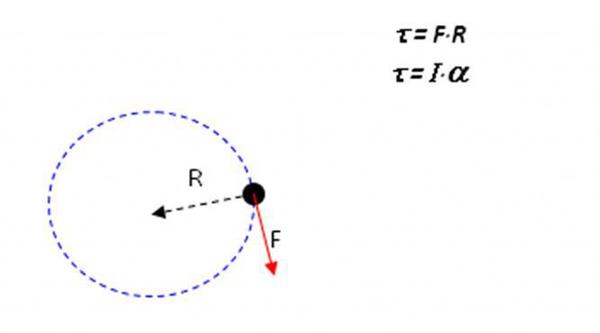
До того як привести формулювання теореми Штейнера, слід розібратися з самим поняттям моменту інерції. Припустимо, є деяке тіло певної маси і довільної форми. Цим тілом може бути, як матеріальна точка, так і будь-двомірний і тривимірний об’єкт (стрижень, циліндр, куля і т. д.). Якщо аналізований об’єкт здійснює круговий рух навколо деякої осі з постійним кутовим прискоренням α, тоді можна записати наступне рівняння:
M = I*α
Тут величина M представляє сумарний момент сил, який надає прискорення α всій системі. Коефіцієнт пропорційності між ними – I, називається моментом інерції. Ця фізична величина розраховується за такою загальною формулою:
I = ∫m (r2*dm)
Тут r – це дистанція між елементом з масою dm і віссю обертання. Цей вираз означає, що необхідно знайти суму добутків квадратів відстаней r2 на елементарну масу dm. Тобто момент інерції не є чистою характеристикою тіла, що його відрізняє від лінійної інерції. Він залежить від розподілу маси по всьому об’єкту, який обертається, а також від відстані до осі і від орієнтації тіла відносно неї. Наприклад, стрижень буде мати різний I, якщо його обертати щодо центру мас і щодо кінця.
Момент інерції і теорема Штейнера

Відомий швейцарський математик Якоб Штейнер, довів теорему про паралельних осях і моменті інерції, яка тепер носить його прізвище. Ця теорема постулює, що момент інерції для абсолютно будь-якого твердого тіла довільної геометрії щодо деякої осі обертання дорівнює сумі моменту інерції відносно осі, яка перетинає центр мас тіла і паралельна першої, і добутку маси тіла на квадрат відстані між цими осями. Математично ця формулювання записується так:
IZ = IO + m*l2
IZ і IO – моменти інерції щодо осі Z і паралельної їй осі O, яка проходить через центр мас тіла, l – відстань між прямими Z O.
Теорема дозволяє, знаючи величину IO, розрахувати будь-який інший момент IZ відносно осі, яка паралельна O.
Доказ теореми
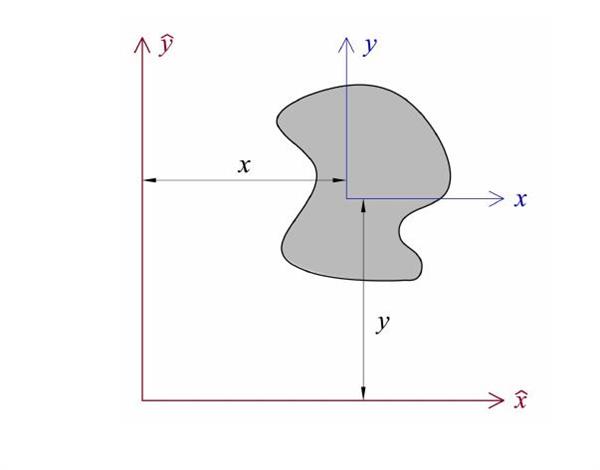
Формулу теореми Штейнера можна легко отримати самостійно. Для цього розглянемо довільне тіло на площині xy. Нехай початок координат проходить через центр мас цього тіла. Розрахуємо момент інерції IO яка проходить через початок координат перпендикулярно площині xy. Оскільки відстань до будь-якої точки тіла виражається формулою r = √ (x2 + y2), тоді одержуємо інтеграл:
IO = ∫m (r2*dm) = ∫m ( (x2+y2) *dm)
Тепер перемістимо паралельно вісь вздовж осі x на відстань l, наприклад, у позитивному напрямку, тоді розрахунок для нової осі моменту інерції буде виглядати наступним чином:
IZ = ∫m (( (x+l)2+y2)*dm)
Розкриємо повний квадрат у дужках і розділимо подынтегральные суми, отримаємо:
IZ = ∫m ( (x2+l2+2*x*l+y2)*dm) = ∫m ( (x2+y2)*dm) + 2*l*∫m (x*dm) + l2*∫mdm
Перше з цих доданків є величиною IO, третій доданок, після проведення інтегрування, дає член l2*m, а ось другий доданок дорівнює нулю. Обнулення вказаного інтегралу пов’язано з тим, що він береться від твору іксів на елементи маси dm, що в середньому дає нуль, так як центр мас знаходиться в початку координат. У результаті, виходить формула теореми Штейнера.
Розглянутий випадок на площині можна узагальнити на об’ємне тіло.
Перевірка формули Штейнера на прикладі стрижня
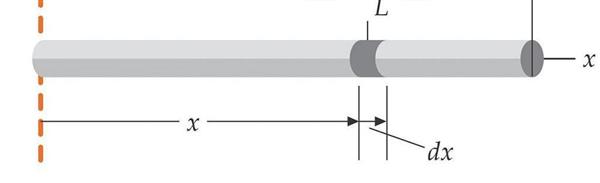
Наведемо простий приклад, на якому продемонструємо, як користуватися розглянутої теоремою.
Відомо, що для стрижня довжиною L і масою m момент інерції IO (вісь проходить через центр мас) дорівнює m*L2/12, а момент IZ (вісь проходить через кінець стрижня) дорівнює m*L2/3. Перевіримо ці дані, скориставшись теоремою Штейнера. Оскільки відстань між двома осями дорівнює L/2, тоді отримуємо момент IZ:
IZ = IO + m*(L/2)2 = m*L2/12 + m*L2/4 = 4*m*L2/12 = m*L2/3
Тобто ми перевірили формулу Штейнера і отримали таке ж значення для IZ, що і в джерелі.
Аналогічні обчислення можна проводити і для інших тіл (циліндра, кулі, диска), отримуючи при цьому необхідні моменти інерції, і не виконуючи інтегрування.
Момент інерції і перпендикулярні осі
Розглянута теорема стосується паралельних осей. Для повноти інформації корисно також привести теорему для перпендикулярних осей. Вона формулюється так: для плоского об’єкта довільної форми момент інерції щодо перпендикулярній йому осі дорівнює сумі двох моментів інерції відносно двох взаємно перпендикулярних і лежать в площині об’єкта осей, при цьому всі три осі повинні проходити через одну точку. Математично це записується так:
Iz = Ix + Iy
Тут z, x, y – три взаємно перпендикулярні осі обертання.
Істотна відмінність цієї теореми від теореми Штейнера полягає в тому, що вона застосовна лише до плоским (двовимірним) твердим об’єктів. Тим не менше на практиці її досить широко використовують, подумки розрізаючи тіло на окремі шари, а потім, складаючи отримані моменти інерції.

