Кожен звертав увагу на все різноманіття видів руху, з якими він стикається у своєму житті. Проте будь-який механічний рух тіла зводиться до одного з двох типів: лінійне або обертальний. Розглянемо в статті основні закони руху тел.
Про яких типах руху піде мова?
Як було зазначено у вступі, всі види руху тіла, які розглядаються в класичній фізиці, пов’язані або з прямолінійною траєкторією, або з круговою. Будь-які інші траєкторії можна отримати завдяки комбінації цих двох. Далі в статті будуть розглянуті наступні закони руху тіла:
- Рівномірний по прямій лінії.
- Равноускоренное (равнозамедленное) по прямій лінії.
- Рівномірний по колу.
- Равноускоренное по колу.
- Рух по еліптичній траєкторії.
Рівномірний рух, або стан спокою
Цим рухом з наукової точки зору почав цікавитися Галілей вперше в кінці XVI – початку XVII століття. Вивчаючи інерційні властивості тіла, а також ввівши поняття про систему відліку, він здогадався, що стан спокою і рівномірного руху – це одне і те ж (все залежить від вибору об’єкта, щодо якого розраховують швидкість).
Згодом Ісаак Ньютон сформулював свій перший закон руху тіла, згідно з яким швидкість останнього є постійною величиною завжди, коли немає зовнішніх сил, що змінюють характеристики руху.

Рівномірний прямолінійний переміщення тіла в просторі описується наступною формулою:
s = v * t
Де s – відстань, яку подолає тіло за час t, рухаючись зі швидкістю v. Це просте вираження також записується в наступних формах (все залежить від величин, які відомі):
v = s / t; t = s / v
Переміщення по прямой з прискоренням
Згідно другого закону Ньютона, наявність зовнішньої сили, яка діє на тіло, неминуче призводить до появи прискорення в останнього. З визначення прискорення (швидкість зміни швидкості) випливає вираз:
a = v / t, або v = a * t
Якщо діюча на тіло зовнішня сила буде залишатися постійною (не буде змінювати модуля і напрями), то прискорення також не зміниться. Такий тип руху називається рівноприскореним, де прискорення виступає коефіцієнтом пропорційності між швидкістю і часом (швидкість зростає лінійно).
Для цього руху пройдений шлях розраховується з допомогою інтегрування швидкості за часом. Закон руху тіла для шляху при рівноприскореному переміщенні набуває форму:
s = a * t2 / 2
Найпоширенішим прикладом цього руху є падіння будь-якого предмета з висоти, при якому сила тяжіння повідомляє йому прискорення g = 9,81 м/с2.

Прямолінійне прискорене (уповільнений) рух з наявністю початкової швидкості
По суті, йдеться про комбінацію двох видів переміщення, розглянутих в попередніх пунктах. Уявімо просту ситуацію: автомобіль їхав з деякою швидкістю v0, потім водій натиснув на гальма, і транспортний засіб через деякий час зупинився. Як описати рух в цьому випадку? Для функції швидкості від часу справедливо вираз:
v = v0 – a * t
Тут v0 – початкова швидкість (до гальмування авто). Знак мінус свідчить про те, що зовнішня сила (тертя ковзання) направлена проти швидкості v0.

Як і в попередньому пункті, якщо взяти інтеграл по часу від v(t), отримуємо формулу для шляху:
s = v0 * t – a * t2 / 2
Відзначимо, що за цією формулою обчислюється тільки шлях гальмування. Щоб дізнатися відстань, пройдену автомобілем за весь час його руху, слід знайти суму двох шляхів: для рівномірного і для равнозамедленного руху.
В описаному вище прикладі, якщо б водій натиснув не на педаль гальма, а на педаль газу, тоді в представлених формулах помінявся б знак “-” на “+”.
Рух по колу
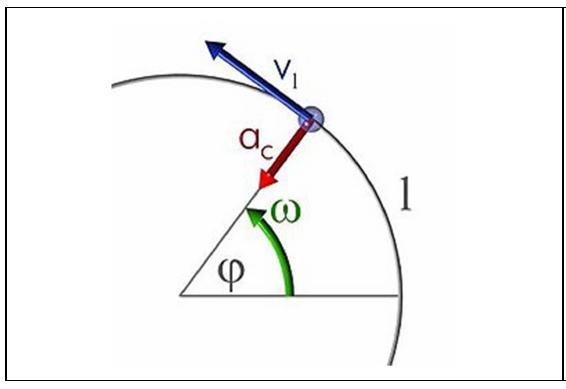
Будь-який рух по колу не може відбуватися без прискорення, оскільки навіть при збереженні модуля швидкості змінюється її напрямок. Прискорення, яке пов’язане з цією зміною, називається доцентровим (саме воно викривляє траєкторію тіла, перетворюючи її в коло). Модуль прискорення цього обчислюють так:
ac = v2 / r, r – радіус
У цьому виразі швидкість може залежати від часу, як це відбувається у випадку равноускоренного руху по колу. В останньому випадку ac буде швидко рости (квадратична залежність).
Центростремительное прискорення визначає силу, яку потрібно прикласти, щоб утримувати тіло на круговій орбіті. Прикладом є змагання з метання молота, коли спортсмени прикладають значні зусилля, щоб розкрутити снаряд до його метання.

Обертання навколо осі з постійною швидкістю
Цей вид руху ідентичний попередньому, тільки описувати його прийнято з використанням лінійних фізичних величин, а з застосуванням кутових характеристик. Закон обертального руху тіла, коли кутова швидкість не змінюється, в скалярної формі записується так:
L =I * ω
Тут L і I – моменти імпульсу та інерції, відповідно, ω – кутова швидкість, яка пов’язана з лінійною рівністю:
v = ω * r
Величина ω показує, на скільки радіан повернеться тіло за секунду. Величини L і I мають такий самий сенс, як імпульс і маса для прямолінійного руху. Відповідно, кут θ, на який повернеться тіло за час t, обчислюється так:
θ = ω * t
Прикладом цього типу руху є обертання маховика, що знаходиться на колінчастому валі у двигуні автомобіля. Маховик – це масивний диск, якому дуже важко дати яке-небудь прискорення. Завдяки цьому він забезпечує плавність зміни крутного моменту, що передається від двигуна до коліс.

Обертання навколо осі з прискоренням
Якщо до системи, яка здатна обертатися, прикладати зовнішню силу, то вона почне збільшувати свою кутову швидкість. Така ситуація описується наступним закону руху тіла навколо осі обертання:
F * d = I * dω / dt
Тут F – зовнішня сила, яка прикладена до системи на відстані d від осі обертання. Твір в лівій частині рівності носить назву моменту сили.
Для равноускоренного руху по колу отримуємо, що ω залежить від часу наступним чином:
ω = α * t, де α = F * d / I – кутове прискорення
В цьому випадку кут повороту за час t, можна визначити, проинтегрировав ω по часу, тобто:
θ = α * t2 / 2
Якщо ж тіло оберталося вже з деякою швидкістю ω0, а потім почав діяти зовнішній момент сили F*d, то за аналогією з лінійним випадком можна записати такі вирази:
ω = ω0 + α * t;
θ = ω0 * t + α * t2 / 2
Таким чином, поява зовнішнього моменту сил є причиною наявності прискорення в системі з віссю обертання.
Для повноти інформації зазначимо, що змінити швидкість обертання ω можна не тільки за допомогою зовнішнього моменту сил, але й завдяки зміні внутрішніх характеристик системи, зокрема її моменту інерції. Цю ситуацію бачив кожен чоловік, який спостерігав за обертанням фігуристів на льоду. Групуючись, спортсмени збільшують ω за рахунок зменшення І, відповідно простого закону руху тіла:
I * ω = const
Рух по еліптичній траєкторії на прикладі планет Сонячної системи
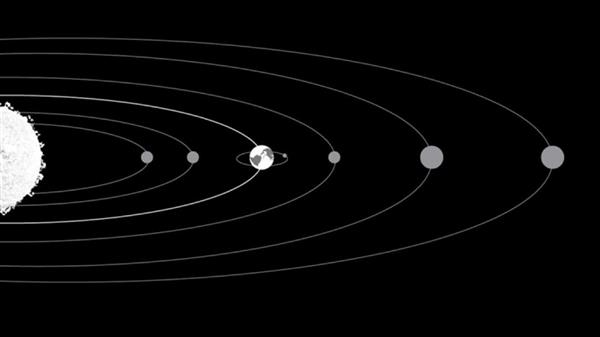
Як відомо, наша Земля та інші планети Сонячної системи обертаються навколо своєї зірки не по колу, а по еліптичній траєкторії. Вперше математичні закони для опису обертання сформулював знаменитий німецький учений Йоганн Кеплер на початку XVII століття. Використовуючи результати спостережень свого вчителя Тихо Бразі за рухом планет Кеплера, прийшов до формулювання своїх трьох законів. Вони формулюються наступним чином:
- Планети Сонячної системи рухаються по еліптичних орбітах, причому Сонце розташоване в одному з фокусів еліпса.
- Радіус-вектор, який з’єднує Сонце і планету, за рівні проміжки часу описує однакові площі. Цей факт випливає з збереження моменту імпульсу.
- Якщо поділити квадрат періоду обігу на куб великої півосі еліптичної орбіти планети, то виходить деяка константа, яка однакова для всіх планет нашої системи. Математично це записується так:
T2 / a3 = С = const
Згодом Ісаак Ньютон, використовуючи ці закони руху тіл (планет), сформулював свій знаменитий закон всесвітньої гравітації, або тяжіння. Застосовуючи його, можна показати, що константа C у 3-му законі Кеплера дорівнює:
C = 4 * pi2 / (G * M)
Де G – гравітаційна універсальна константа, а M – маса Сонця.
Зазначимо, що рух по еліптичній орбіті в разі дії центральної сили (тяжіння) призводить до того, що лінійна швидкість v постійно змінюється. Вона максимальна, коли планета перебуває найближче до зірки, і мінімальна далеко від неї.

