Однією з найбільш простих об’ємних фігур є трикутна піраміда, оскільки вона складається з найменшого числа граней, з якого можна утворити фігуру у просторі. У цій статті розглянемо формули, за допомогою яких можна знайти об’єм правильної трикутної піраміди.
Трикутна піраміда
Згідно із загальним визначенням піраміда являє собою багатокутник, всі вершини якого з’єднані з однією точкою, не розташованої в площині цього багатокутника. Якщо останній являє собою трикутник, то вся фігура називається трикутною пірамідою.
Розглянута піраміда складається з підстави (трикутника) і трьох бічних граней (трикутників). Точка, в якій поєднано три бічні грані, називається вершиною фігури. Опущений на підставу перпендикуляр з цієї вершини є висотою піраміди. Якщо точка перетину перпендикуляра з підставою збігається з точкою перетину медіан трикутника в основі, тоді говорять про правильній піраміді. В іншому випадку вона буде похилою.
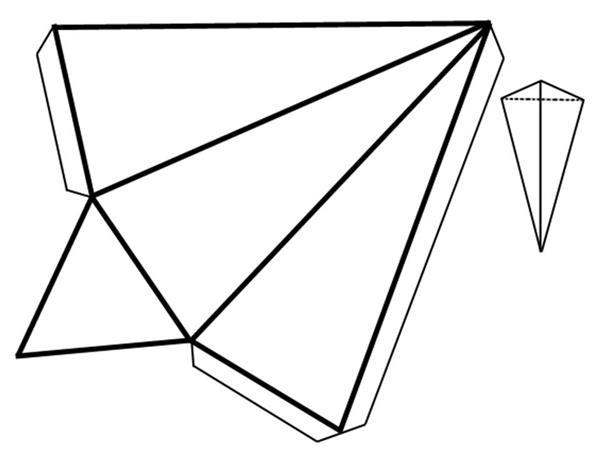
Як було сказано, підстава трикутної піраміди може представляти собою трикутник загального типу. Однак якщо він є рівностороннім, а сама піраміда прямій, тоді говорять про правильної об’ємної фігури.
Будь-яка трикутна піраміда має 4 грані, 6 ребер і 4 вершини. Якщо довжина всіх ребер рівні між собою, тоді така фігура називається тетраедром.
Об’єм трикутної піраміди загального типу
Перш ніж записати формулу обсягу правильної трикутної піраміди, наведемо вираз цієї фізичної величини для піраміди загального типу. Цей вираз має вигляд:
V = 1/3*So*h.
Тут So – площа підстави, h – висота фігури. Це рівність буде справедливим для будь-якого типу підстави багатокутника піраміди, а також для конуса. Якщо ж у підставі знаходиться трикутник, який має довжину сторони a і висоту ho, опущену на неї, тоді формула для обсягу запишеться так:
V = 1/6*a*ho*h.
Формули об’єму правильної трикутної піраміди
Правильна трикутна піраміда має рівносторонній трикутник в підставі. Відомо, що висота цього трикутника пов’язана з довжиною його сторони рівністю:
ho = √3/2*a.
Підставляючи цей вираз у формулу для об’єму трикутної піраміди, записану в попередньому пункті, отримуємо:
V = 1/6*a*ho*h = √3/12*a2*h.
Об’єм правильної піраміди з трикутним підставою є функцією довжини сторони основи і висоти фігури.
Оскільки будь-правильний многокутник можна вписати в коло, радіус якої однозначно визначить довжину сторони багатокутника, тоді цю формулу можна записати через відповідний радіус r:
V = √3/4*h*r2.
Цю формулу легко отримати з попередньої, якщо врахувати, що радіус r описаного кола через довжину сторони трикутника a визначається виразом:
r = a/√3.
Завдання на визначення об’єму тетраедра
Покажемо, як використовувати наведені вище формули при розв’язуванні конкретних задач геометрії.
Відомо, що тетраедр має довжину ребра 7 див. Знайдіть об’єм правильної трикутної піраміди-тетраедра.
Нагадаємо, що тетраедр є правильної трикутною пірамідою, в якій всі підстави рівні між собою. Щоб скористатися формулою обсягу правильної трикутної піраміди, необхідно обчислити дві величини:
- довжину сторони трикутника;
- висоту фігури.
Перша величина відома з умови задачі:
a = 7 див.
Щоб визначити висоту, розглянемо фігуру, зображену на малюнку.
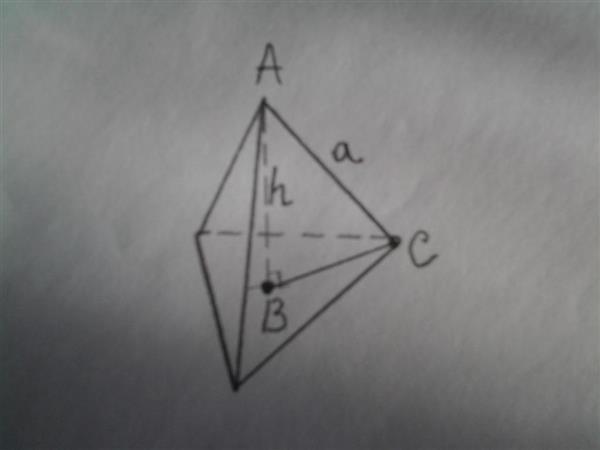
Зазначений трикутник ABC є прямокутним, де кут ABC дорівнює 90o. Сторона AC – це гіпотенуза, довжина якої дорівнює a. Шляхом нескладних геометричних міркувань можна показати, що сторона BC має довжину:
BC = a/√3.
Зауважимо, що довжина BC є радіусом описаного навколо трикутника кола.
Висоту піраміди h можна розрахувати, застосовуючи теорему Піфагора. Маємо:
h = AB = √(AC2 – BC2) = √(a2 – a2/3) = a*√(2/3).
Тепер можна h і a підставити у відповідну формулу для об’єму:
V = √3/12*a2*a*√(2/3) = √2/12*a3.
Таким чином, ми отримали формулу об’єму тетраедра. Видно, що обсяг залежить тільки від довжини ребра. Якщо у рівняння підставити значення з умови задачі, тоді отримуємо відповідь:
V = √2/12*73 ≈ 40,42 см3.
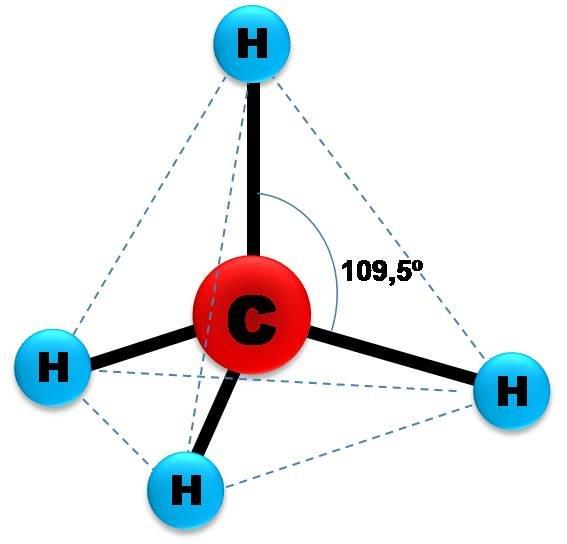
Якщо порівняти цю величину з об’ємом куба, мають таке ж ребро, то отримаємо, що об’єм тетраедра в 8,5 разів менше. Це свідчить про те, що тетраедр є компактною фігурою, яка реалізується у деяких природних речовинах. Наприклад, молекула метану має тетраэдрическую форму, а кожний атом вуглецю в алмазі з’єднаний з чотирма іншими атомами, що утворюють тетраедр.
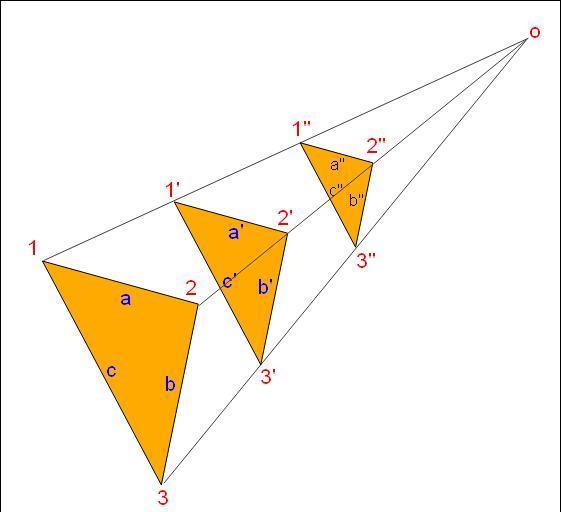
Завдання з гомотетичными пірамідами
Вирішимо одну цікаву геометричну задачу. Припустимо, що є правильна трикутна піраміда з деяким об’ємом V1. У скільки разів слід зменшити розміри цієї фігури, щоб отримати гомотетичную їй піраміду з обсягом, в три рази меншим вихідного?
Завдання почнемо вирішувати з запису формули для вихідної правильної піраміди:
V1 = √3/12*a12*h1.
Нехай необхідний за умовами задачі об’єм фігури вийде, якщо помножити її параметри на коефіцієнт k. Маємо:
V2 = √3/12*k2*a12*k*h1 = k3*V1.
Оскільки з умови відомо відношення обсягів фігур, то отримуємо значення коефіцієнта k:
k = ∛(V2/V1) = ∛(1/3) ≈ 0,693.
Відзначимо, що аналогічне значення коефіцієнта k ми б отримали для піраміди довільного типу, а не тільки для правильної трикутної.

