Ознайомившись з матеріалом, читач зрозуміє, що планіметрія – це зовсім не складно. У статті наведено найважливіша теоретична інформація та необхідні для вирішення конкретних завдань формули. По полицях розкладені важливі затвердження та властивості фігур.
Визначення і важливі факти
Планіметрія – це розділ геометрії, який розглядає об’єкти на плоскій двовимірної поверхні. Можна виділити деякі відповідні приклади: квадрат, коло, ромб.
Серед усього іншого варто виділити точку і пряму. Вони є двома основними поняттями планіметрії.

Вже на них будуються всі решта, наприклад:
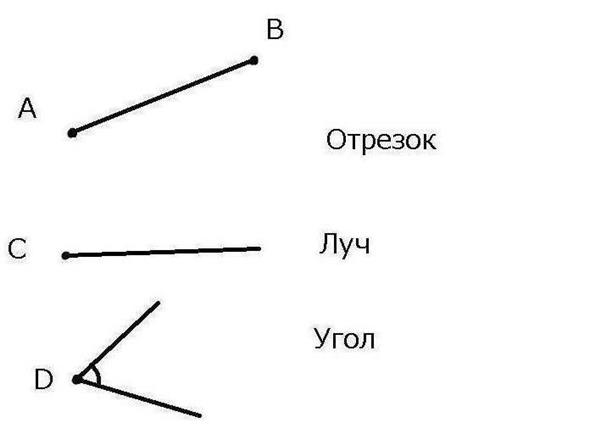
- Відрізок – це частина прямої лінії, обмежена двома точками.
- Промінь – об’єкт, аналогічний відрізку, проте, має кордон лише з одного боку.
- Кут, який складається з двох променів, що виходять з однієї точки.

Аксіоми і теореми
Докладніше розберемося з аксіомами. У планіметрії це найважливіші правила, за якими працює вся наука. Та й не тільки в ній. За визначенням, мова йде про твердженнях, які не потребують доказів.
Аксіоми, які буду розглянуті нижче, входять в так звану Евклидовую геометрію.
- Є дві точки. Через них завжди можна провести єдину пряму.
- Якщо існує пряма, тобто точки, які на ній лежать, і точки, що не лежать на ній.
Це 2 твердження називають аксіомами приналежності, а наступні – порядку:
- Якщо на прямій розташовані три точки, то одна з них обов’язково знаходиться між двома іншими.
- Площина ділиться будь-якої прямої на дві частини. Коли кінці відрізка лежать на одній половині, то значить і весь об’єкт належить їй. В іншому випадку вихідна пряма і відрізок мають точку перетину.
Аксіоми заходів:
- Кожен відрізок має довжину, відмінну від нуля. Якщо точка розбиває його на кілька частин, то їх сума буде дорівнює повній довжині об’єкта.
- У кожного кута є певна градусна міра, яка не дорівнює нулю. Якщо розбити його променем, то вихідний кут дорівнюватиме сумі освічених.
Паралельність:
- На площині пряма розташована. Через будь-яку точку, що не належить їй, можна провести лише одну пряму, паралельну даній.
Теореми в планіметрії – це вже не зовсім фундаментальні твердження. Зазвичай їх приймають як факт, але кожна з них має доказ, побудована на основних поняттях, згаданих вище. Крім того, їх дуже багато. Розібрати все буде досить важко, але в представленому матеріалі будуть присутні деякі з них.
З наступними двома варто ознайомитися раніше:
- Сума суміжних кутів дорівнює 180 градусам.
- Вертикальні кути мають однакову величину.
Ці дві теореми можуть стати в нагоді в рішенні геометричних задач, пов’язаних з n-косинцями. Вони досить прості і інтуїтивно зрозумілі. Варто їх запам’ятати.
Трикутники
Трикутник – це геометрична фігура, що складається з трьох послідовно з’єднаних відрізків. Класифікують їх за кількома ознаками.
По боках (співвідношення випливають з назв):
- Рівносторонній.
- Рівнобедрений – дві сторони і протилежні їм кути відповідно рівні.
- Різнобічний.

По кутах:
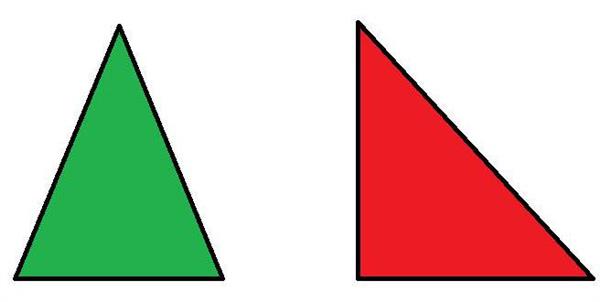
- гострокутний;
- прямокутний;
- тупокутний.
Два кута незалежно від ситуації завжди будуть гострими, а третій визначається першою частиною слова. Тобто у прямокутного трикутника, один з кутів дорівнює 90 градусам.
Властивості:
- Чим більше кут, тим більше протилежна йому сторона.
- Сума всіх кутів – 180 градусів.
- Площа можна обчислити за формулою: S = ½ ⋅ h ⋅ a, де a – сторона, h – проведена до неї висота.
- Завжди можна вписати окружність у трикутник або ж описати її навколо нього.
Про одну з основних формул планіметрії говорить теорема Піфагора. Працює вона виключно для прямокутного трикутника і звучить так: квадрат гіпотенузи дорівнює сумі квадратів катетів: AB2 = AC2 + BC2.
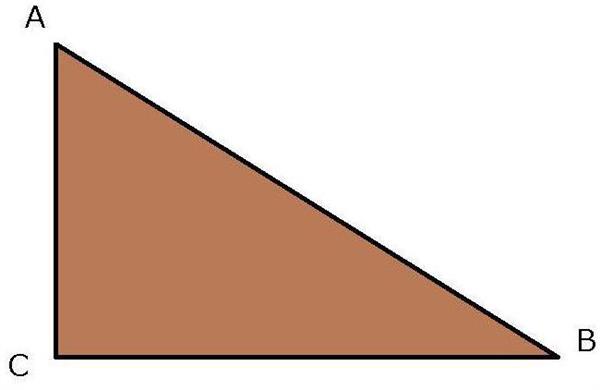
Під гіпотенузою розуміють сторону, протилежну куті 90°, а під катетами – прилеглі.
Чотирикутники
Інформації на цю тему надзвичайно багато. Нижче наведено лише найважливіша.
Деякі різновиди:
- Паралелограм – протилежні сторони рівні і попарно паралельні.
- Ромб – паралелограм, чиї сторони мають однакову довжину.
- Прямокутник – це паралелограм з чотирма прямими кутами
- Квадрат – ромб і прямокутник.
- Трапеція – лише дві протилежні сторони паралельні.
Властивості:
- Сума внутрішніх кутів дорівнює 360 градусів.
- Площа завжди можна обчислити за формулою: S=√(p-a)(p-b)(p-c)(p-d), де p – половина периметра, a, b, c, d – сторони фігури.
- Якщо навколо чотирикутника можна описати коло, тоді його називають опуклим, якщо немає – невыпуклым.