Серед усіх послідовностей чисел геометрична прогресія, яку розглядають у курсі алгебри 9 класу, є однією з найвідоміших. Що вона собою представляє і як вирішити геометричну прогресію — на ці питання дано відповідь в даній статті.
Послідовність чисел, яка підпорядковується математичного закону

Назва цього пункту є загальним визначенням геометричній прогресії. Закон, яким вона описується, є доволі простим: кожне наступне число відрізняється від попереднього на множник, який отримав назву “знаменник”. Можна позначити його буквою r. Тоді можна записати наступне рівняння:
an+1 = an*r.
Тут an – член прогресії з номером n.
Якщо r буде більше 1, то прогресія буде зростати по модулю (вона може убувати, якщо перший її член буде мати негативний знак). Якщо r буде менше одиниці, тоді вся прогресія буде прагнути до нуля або знизу (a1<0), або зверху (a1>0). У разі негативного знаменника (r<0) мати місце буде чергується числова послідовність (кожен позитивний член буде оточений двома негативними). Нарешті, при рівності r одиниці вийде простий набір чисел, який, як правило, не називають прогресією.
Приклад розглядуваного виду прогресії наведено нижче:
2, 3, 4, 5, 6, 75, …
Тут перший член дорівнює 2, а знаменник дорівнює 1,5.
Важливі формули
Як у 9 класі вирішувати геометричну прогресію? Для цього слід знати не тільки її визначення і розуміти, про що йде мова, але й запам’ятати дві важливі формули. Перша з них наводиться нижче:
an = a1*rn-1.
Вираз дозволяє без особливих зусиль знайти довільний елемент послідовності, проте для цього необхідно знати два числа: знаменник і перший елемент. Довести цю формулу просто, потрібно лише згадати визначення геометричної прогресії: другий елемент виходить множенням першого на знаменник першого ступеня, третій елемент – множенням першого на знаменник у другому ступені і так далі. Корисність цього виразу очевидна: немає потреби в послідовному відновленні всього числового ряду, щоб дізнатися, яке значення прийме його n-й елемент.
Наступна формула є також корисною при відповіді на питання, як вирішувати геометричну прогресію. Мова йде про суму її елементів, починаючи з першого і закінчуючи n-ним. Відповідний вираз наведено нижче:
Sn = a1*(rn-1)/(r-1).
Варто звернути увагу на його особливість: як і у формулі для знаходження n-ного елемента, тут теж досить знати ті ж два числа (a1 r). Цей результат не є дивним, адже кожен член прогресії пов’язаний з означеними числівниками.
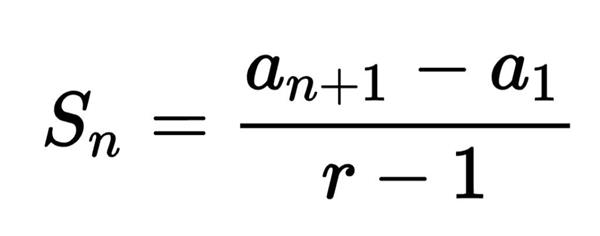
Далі наведено кілька прикладів, в яких показано, як вирішити геометричну прогресію .
Відновлення прогресії
Перший приклад, як вирішувати геометричну прогресію, має наступне умова: відомо, що два числа 10 і 20 утворюють розглянутий вид прогресії. При цьому числа є восьмим і п’ятнадцятим елементами ряду. Необхідно відновити весь ряд, знаючи, що він повинен бути спаданням.
Це дещо заплутана умова завдання слід розібрати уважно: оскільки мова йде про спадаючому ряді, то число 10 повинне стояти в 15 позиції, а 20 – у 8. Приступаючи до вирішення, випишіть для кожного з чисел відповідні рівності:
a8 = a1*r7 і a15 = a1*r14.
Ви маєте два рівності з двома невідомими. Вирішіть їх, висловлюючи з першого a1 і підставляючи його в друге. Вийде:
a1 = a8*r-7 і a15 = a8*r-7 *r14=a8*r7 => r=7√(a15/a8).
Тепер залишається підставити відповідні значення з умови і обчислити корінь сьомий ступеня. Вийде:
r=7√(a15/a8) = 7√(10 /20 ) ≈ 0,9057.
Підставляючи отриманий знаменник в будь-який з виразів для відомого n-ного елемента, виходить a1:
a1 = a8*r-7 = 20*(0,9057)-7 ≈ 40,0073.
Таким чином, ви знайдете перший член і знаменник, що означає, що ви відновите всю прогресію. Перші кілька членів:
40,0073, 36,2346, 32,8177, 29,7230, …
Варто відзначити, що при виконанні розрахунків було використано округлення до 4-х знаків після коми.
Знаходження невідомого члена ряду
Тепер варто розглянути інший приклад: відомо, що сьомий елемент ряду дорівнює 27, чому дорівнює тринадцятий член, якщо знаменник r = -2. Як вирішити геометричну прогресію, користуючись цими даними? Дуже просто, потрібно виписати формулу для 7-го елемента:
a7 = a1*r6.
Оскільки в цьому рівність невідомо тільки число a1, виразіть його:
a1 = a7*r-6.
Скористайтеся останньою рівністю, підставляючи його у формулу для 13-го члена, який необхідно знайти. Вийде:
a13 = a1*r12 = a7*r-6*r12 = a7*r6.
Залишилося підставити числа і записати відповідь:
a13 = a7*r6 = 27*(-2)6 = 1728.
Отримане число демонструє, наскільки швидко зростає геометрична прогресія.
Завдання на суму

Остання задача, яка розкриває питання, як вирішити геометричну прогресію, пов’язана з перебуванням суми декількох елементів. Нехай a1 = 1,5, r = 2. Слід обчислити суму членів цього ряду, починаючи з 5-го і закінчуючи 10-м.
Щоб отримати відповідь на поставлене запитання, слід застосувати формулу:
S510 = S10 – S4.
Тобто спочатку потрібно знайти суму 10 елементів, потім суму перших 4-х і відняти їх між собою. Слідуючи вказаним алгоритмом, вийде:
S10 = a1*(rn-1)/(r-1) = 1,5*(210-1)/(2-1) = 1534,5;
S4 = a1*(rn-1)/(r-1) = 1,5*(24-1)/(2-1) = 22,5;
S510 = 1534,5 – 22,5 = 1512.
Варто відзначити, що в кінцевій формулі віднімалася сума саме 4 доданків, оскільки п’яте за умовою задачі має брати участь в сумі.

