У математиці існує поняття “множина”, так само як і існують приклади зіставлення цих множин між собою. Назвами видів зіставлення множин виступають такі слова: биекция, ін’єкція, сюръекция. Нижче про кожного з них розказано докладніше.
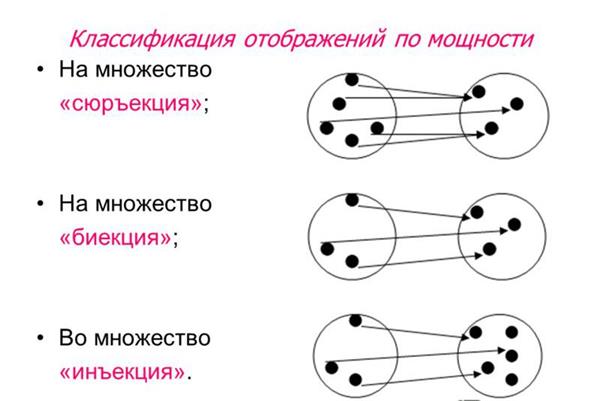
Биекция – це… це що?
Одна група елементів першого безлічі зіставляється з другою групою елементів з другої множини в такому вигляді: кожний елемент першої групи безпосередньо зіставляється з іншим одним елементом з другої групи, і при цьому не виникає ситуації з нестачею або перебором елементів будь-якої з двох груп множин.
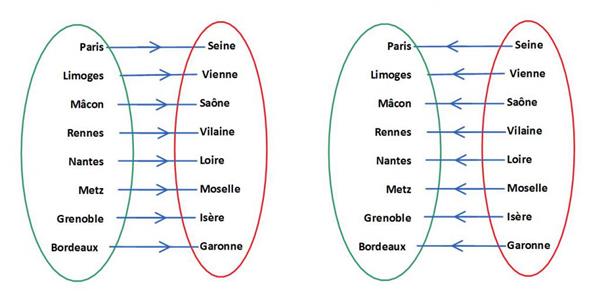
Формулювання основних властивостей:
- Один елемент до одного.
- Не залишається зайвих елементів при зіставленні і зберігається перша властивість.
- Можливо зворотне відображення зіставлення із збереженням загального виду.
- Биекция – це така функція, що є одночасно инъективной і сюръективной.

