Натяг нитки
При вирішенні завдань руху тіла по похилій площині ця сила не завжди присутня. Її поява визначається тим, що знаходиться на похилій площині тіло пов’язано з допомогою нерозтяжній нитці з іншим тілом. Часто друге тіло звисає на нитки через блок за межами площини.
На що знаходиться на площині предмет, сила натягу нитки впливає або прискорюючи його, або сповільнюючи. Все залежить від модулів сил, що діють у фізичній системі.
Поява цієї сили в задачі значно ускладнює процес вирішення, оскільки доводиться розглядати одночасно рух двох тіл (на площині і звисає).

Далі наведемо приклад вирішення двох завдань без участі сили натягу нитки.
Завдання на визначення критичного кута
Тепер настав час застосувати описану теорію для вирішення реальних завдань руху по похилій площині тіла.
Припустимо, що брус з дерева має масу 2 кг Він знаходиться на дерев’яній площині. Слід визначити, при якому критичному вугіллі нахилу площини брус почне по ній ковзати.
Ковзання бруса настане тільки тоді, коли сумарна діюча вниз вздовж площини сила на нього виявиться більше нуля. Таким чином, щоб вирішити цю задачу, досить визначити результуючу силу і знайти кут, при якому вона стане більше нуля. Згідно умові задачі на брус будуть вздовж площини надавати дію тільки дві сили:
- складова сили тяжіння Fg1;
- тертя спокою Ff.
Щоб почалося ковзання тіла, має виконуватися умова:
Fg1 ≥ Ff.
Відзначимо, що якщо складова сили тяжіння перевищить тертя спокою, то вона також буде більше сили тертя ковзання, тобто почався рух буде продовжуватися з постійним прискоренням.
Малюнок нижче показує напрямки всіх діючих сил.
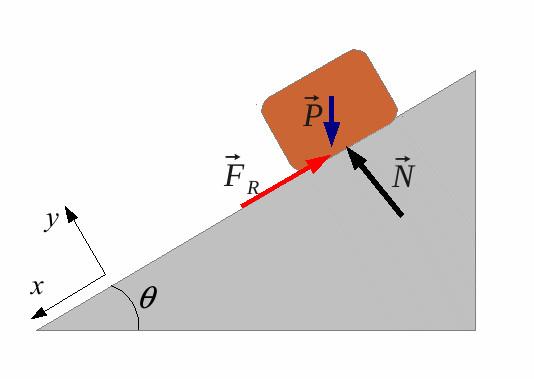
Позначимо критичний кут символом θ. Нескладно показати, що сили Fg1 і Ff будуть рівні:
Fg1 = m × g × sin(θ);
Ff = µ × m × g × cos(θ).
Тут m × g – це вага тіла, µ – коефіцієнт сили тертя спокою для пари матеріалів дерево-дерево. З відповідної таблиці коефіцієнтів можна знайти, що він дорівнює 0,7.
Підставляємо знайдені величини в нерівність, отримуємо:
m × g × sin(θ) ≥ µ × m × g × cos(θ).
Перетворюючи це рівність, приходимо до умови руху тіла:
tg(θ) ≥ µ =>
θ ≥ arctg(µ).
Ми отримали дуже цікавий результат. Виявляється, значення критичного кута θ не залежить від маси тіла на похилій площині, а однозначно визначається коефіцієнтом тертя спокою µ. Підставляючи його значення в нерівність, отримаємо величину критичного кута:
θ ≥ arctg(0,7) ≈ 35o.