Кожен чув про таких об’ємних постатей, як куля, циліндр, піраміда і призма. Остання з них є досконалим полиэдром, властивості якого розглядаються у шкільному курсі геометрії в старших класах. У даній статті розкриємо питання, як знайти об’єм прямої призми, в основі якої лежить довільний багатокутник.
Поняття про прямій призмі
Перед визначенням обсягу будь-просторової фігури важливо чітко розібратися, з чим доведеться мати справу. У нашому випадку ми розглянемо пряму, або прямокутну призму. Вона являє собою фігуру, що складається з двох підстав і кількох бічних граней, які перпендикулярні цих підстав. Обидва підстави представлені одним і тим же гратки і є паралельними один одному. Якщо кількість сторін багатокутника прагне до нескінченності, то така пряма призма переходить в циліндр.
Питання перпендикулярності бічних граней і підстав фігури має принципове значення. Як буде показано нижче, саме від цієї властивості залежить кінцева формула для обчислення об’єму прямої, або прямокутної призми. Прямокутної вона називається тому, що її бічні грані є прямокутниками.
Протилежністю прямокутної призми є косоугольная. Як можна здогадатися, відмінність між ними полягає тільки в куті між бічними гранями і підставами. У косокутних, або похилої призми цей кут відрізняється від 90o.
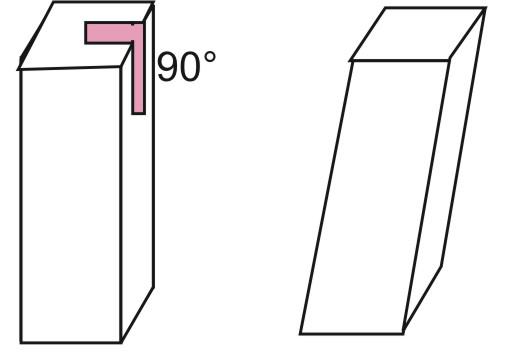
На малюнку вище зображено дві чотирикутні призми, одна з яких є прямий (ліва), а друга – косокутної.
Які прямокутні призми бувають?
Відмінність між усіма прямими призмами полягає в типі багатокутника, що утворює підстави фігур. Гратки з найменшою кількістю сторін є трикутник. Призма, яка побудована за допомогою нього, буде називатися трикутної. Аналогічним чином фігура з чотирикутними підставами отримає назву чотирикутної призми. Міркуючи таким чином, можна сказати, що n-вугільна пряма призма утворена двома n-косинцями і n прямокутниками.
В попередньому абзаці при розгляді назв призм використовувалися довільні трикутники, чотирикутники і n-кутники. Якщо ж розглядається правильний багатокутник, то утворена їм призма також буде називатися правильною. Наприклад, для n = 3 правильним гратки є рівносторонній трикутник, а для n = 4 – квадрат.

Вище на рисунку 6 зображені правильних прямокутних призм. Кожна попередня відрізняється від подальшої наявністю в підставах багатокутника, у якого на 1 вершину і 1 сторону більше. Перша призма є правильної трикутної, а остання – правильної восьмикутної.
Обчислення об’єму прямої призми
Отримавши чітке уявлення про прямокутної призми, можна перейти до обчислення її обсягу. Як знайти об’єм прямої призми? Дуже просто, достатньо лише визначити площу одного з її підстав і висоту фігури, а потім одну величину помножити на іншу. Математична формула для обсягу має вигляд:
V = So*h
Висота фігури h для прямої призми є не що інше, як довжина її бічного ребра (вертикальної сторони прямокутника). Цей факт істотно спрощує розрахунок, оскільки в іншому випадку (коли призма є косокутної) для обчислення висоти h довелося б будувати перпендикуляр від однієї основи до іншої і, враховуючи кут нахилу призми, розраховувати довжину цього перпендикуляра.
Що стосується площі підстави So, то для її визначення слід використовувати геометричні властивості відповідного багатокутника. Наприклад, якщо ним є паралелограм, то його площа обчислюється як добуток підстави на опущену до нього висоту. Величину So простіше вирахувати, якщо багатокутник є правильним.

Формула для об’єму призми
Припустимо, що основу розглянутої об’ємної фігури утворено n-кутником. Із загального курсу геометрії відомо, що площа такого n-кутника розраховується за такою універсальною формулою:
Sn = n/4*a2*ctg(pi/n)
Де символом «a» позначена довжина сторони n-кутника.
Об’єм прямої призми, основою якої є правильний багатокутник з кількістю вершин n, обчислюється з допомогою виразу:
Vn = Sn*h = n/4*ctg(pi/n)*a2*h
Функцію котангенса для кожного випадку можна обчислити, або використовуючи відповідні таблиці тригонометричних функцій, або застосовуючи калькулятор.
Далі в статті розглянемо кілька прикладів використання наведених формул для обчислення об’єму призми.
Завдання №1. Об’єм правильної призми семикутною

Обчислимо обсяг рідко використовується в задачах геометрії призми, підстави якої являють собою правильні семиугольники. Ця фігура зображена на малюнку вище. Запишемо для неї відповідну формулу:
V7 = 7/4*ctg(pi/7)*a2*h
Для визначення котангенса від кута pi/7 скористаємося калькулятором. Тоді отримуємо:
V7 = 7/4*ctg(pi/7)*a2*h = 3,634*a2*h
Наприклад, якщо a = 10 см, h = 7 см, тоді отримуємо об’єм:
V7 = 3,634*102*7 = 2543,8 см3
Тара, виготовлена з цієї призми, здатна вмістити в себе трохи більше 2,5 літрів води.
Завдання №2. Об’єм трикутної призми

Припустимо, що необхідно знайти об’єм прямої призми з прямокутним трикутником в підставі. Нехай катети цього трикутника дорівнюють a і b, а висота фігури становить h. Приклад цієї фігури, зробленої зі скла, показаний на фото вище.
Оскільки основа призми не є правильним трикутником, то використовувати універсальну формулу не можна. Однак можна скористатися властивістю прямокутного трикутника, для якого площа обчислюється як половина добутку його катетів. Враховуючи цей факт, отримуємо вираз:
V = So*h = 1/2*a*b*h
Якщо катети дорівнюють 5 см і 9 см, а висота становить 8 см, тоді розрахований обсяг буде дорівнює 180 см3.

