Циліндр – це одна з просторових фігур, яка є об’єктом вивчення стереометрії. Важлива характеристика будь-якої фігури – це площа її поверхні. У цій статті розглянемо, що собою являє розгортка циліндра, а також покажемо, як обчислити її площу.
Циліндр як фігура геометрії
Припустимо, що у нас є деяка плавна крива. Це може бути коло, еліпс, парабола і так далі. Візьмемо відрізок довільної довжини, який не лежить в площині кривої, і опишемо за допомогою нього поверхню, дотримуючись напрямку кривої і транслюючи відрізок паралельно самому собі. Отримана поверхня називається циліндричної або просто циліндром. Зазначена крива називається директрисою (напрямної), а відрізок – генератрисой (твірної).
Якщо до циліндричної поверхні додати ще дві плоскі однакові фігури, що обмежують цю поверхню з торців, то отримане тіло також називається циліндром. Воно складається з двох рівних підстав і циліндричної поверхні.
Для наочного уявлення описаної фігури нижче наведено малюнок. На ньому зображений еліптичний циліндр, що має півосі a і b і висоту h (дистанція між підставами).
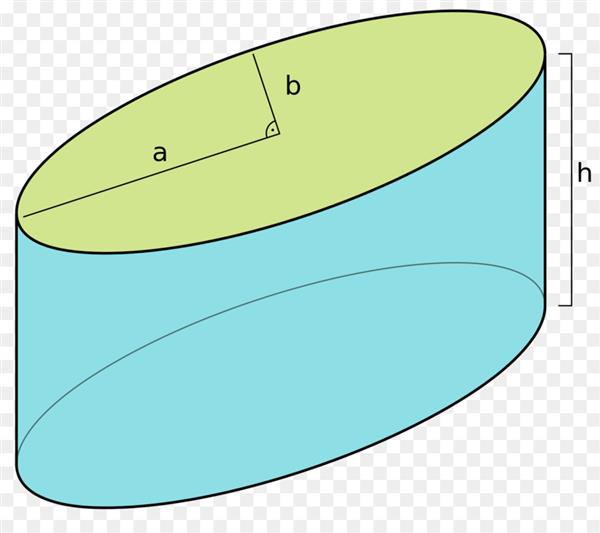
Круглий прямий циліндр
Нехай директрисою буде окружність деякого радіуса. Тоді утворена генератрисой фігура буде називатися круглим циліндром. Тим не менш генератриса відносно площини, обмеженої директрисою, може бути спрямована довільним чином. Тому в загальному випадку говорять про похилому круглому циліндрі. Якщо ж генератриса буде перпендикулярна площинах підстави, то циліндр називається прямим. Він показаний на малюнку нижче.
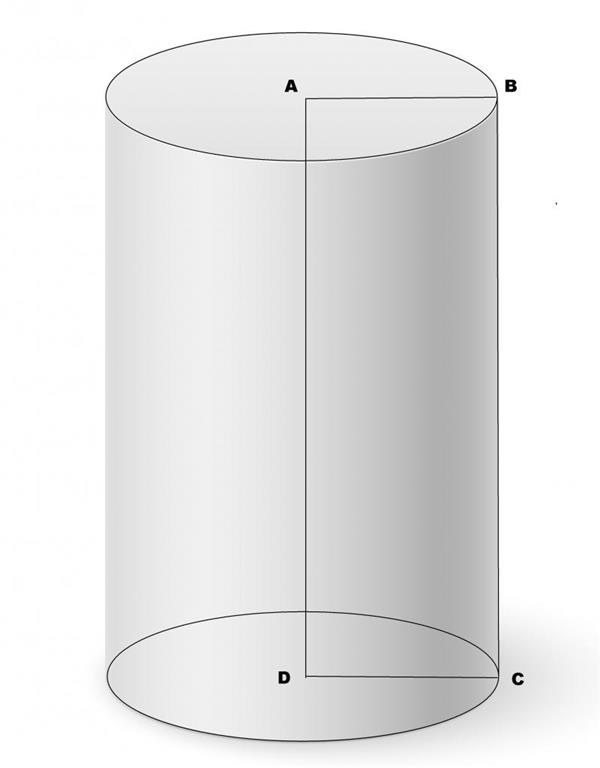
Тут AB = DC – радіус циліндра, AD = BC = h – висота фігури. Для прямого циліндра висота завжди дорівнює довжині утворюючої. Відрізок AD позначає вісь циліндра – пряма, що з’єднує дві центральні точки підстав. Від осі циліндра всі точки бічній поверхні лежать на одній відстані, рівному радіусу фігури.
Далі в статті будемо розглядати розгортку поверхні циліндра, круглого і прямого.
Розгортка круглого прямого циліндра
Коли говорять про розгортці циліндра, то мають на увазі загальну площу його поверхні, представлену плоскими фігурами. Круглий прямий циліндр утворений двома колами, мають однакові радіуси, і однією бічною поверхнею, що ці кола з’єднує один з одним.

На малюнку показаний паперовий циліндр. Як здійснюється побудова розгортки циліндра? Візьмемо уявні ножиці і відріжемо одна підстава уздовж окружності. Потім зробимо аналогічні дії з другим підставою. Бічну поверхню разрєжєм уздовж генератрисы, тобто паралельно осі фігури, і розгорнемо її. Таким чином, ми отримали розгортку, яка показана на малюнку нижче.
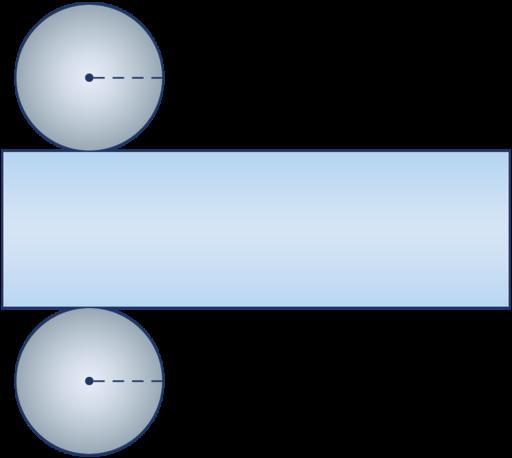
Очевидно, що вона складається з двох однакових кіл. Що стосується циліндричної поверхні, то в розрізаному вигляді вона представлена прямокутником. Розгортку зручно використовувати при визначенні площі поверхні розглянутої фігури.
Площа розгортки циліндра
Вище ми показали, як можна отримати розгортку фігури. Щоб розрахувати її площа, необхідно скласти площі всіх її частин, тобто для двох круглих підстав і одного прямокутника.
Позначимо радіус основи буквою r, а висоту фігури – літерою h. Площа однієї підстави дорівнює площі кола, тобто:
So = pi*r2
Тут pi – число Пі, приблизно дорівнює 3,14.
Щоб обчислити площу прямокутника, що представляє бічну поверхню фігури в розгорнутому вигляді, необхідно знати дві його сторони. Одна з них дорівнює висоті h. Друга, як можна здогадатися, відповідає довжині директриси, тобто довжині кола. Позначимо її l. Тоді можна записати такі рівності:
l = 2*pi*r;
Sb = l*h = 2*pi*r*h
Тут Sb – площа прямокутника, рівна площі циліндричної поверхні.
Враховуючи, що фігура має дві підстави, складаємо розраховані величини, отримуємо загальну площу розгортки циліндра:
S = 2*So + Sb = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r + h)
Площа S фігури однозначно визначається через її радіус і висоту.
Покажемо, як використовувати це рівність для вирішення геометричної задачі.
Завдання на знаходження радіусу фігури
Відомо, що загальна поверхня круглого прямого циліндра становить 60 см2. Чому дорівнює радіус основи циліндра, якщо його висота дорівнює 7 см, а фігура має лише одну підставу.
Описаний в умові задачі циліндр являє собою бочку без кришки, тому площа його поверхні утворена не двома, а одним підставою.

Якщо врахувати названий факт, тоді формула для площі фігури запишеться в наступному вигляді:
S = pi*r2 + 2*pi*r*h
Підставимо всі відомі з умови величини в цю рівність, одержимо:
60 = 3,14*r2 + 43,96*r =>
3,14*r2 + 43,96*r – 60 = 0
Ми отримали класичне повне квадратне рівняння. Його вирішення дасть шукане значення радіуса r. Вирішуємо через дискриминант:
D = 43,962 – 4*3,14*(- 60) ≈ 2686,08;
r = (-43,96±√2686,08)/(2*3,14) = 1,25 см
При вирішенні рівняння від’ємний корінь був відкинутий, на увазі його нефізичної значення.
Таким чином, параметри відкритого циліндра з умови задачі становлять 7 см у висоту і 2,5 см в діаметрі.

