Рівномірний рух по прямій лінії
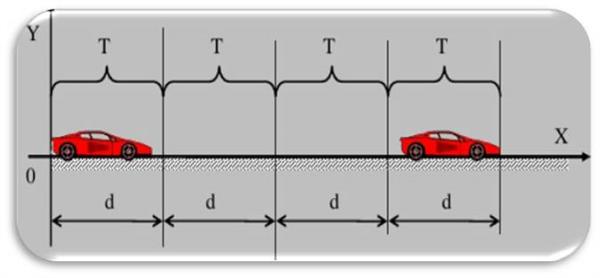
Це ідеалізований тип руху, який передбачає, що тіло протягом деякого проміжку часу рухається вздовж прямої в просторі. При цьому швидкість тіла не змінюється. Позначаючи пройдений шлях символом l, отримуємо формулу:
l = v*t.
Тут v = const.
Цей тип руху розглядався ще філософи Античної Греції. Вони вважали, що для руху тіл необхідно прикласти певну силу, тому природним станом усіх навколишніх об’єктів є спокій. Тільки з приходом епохи Відродження завдяки працям Галілея і Ньютона було показано, що якщо на тіло не діють зовнішні сили, то рівномірність і прямолінійність його руху не порушується.
Швидкість при русі по прямій з прискоренням

Коли з’являється зовнішня сила, то її дія на тіло приводить до зміни швидкості тіла. У динаміці ця ситуація описується другим законом Ньютона:
F = m*a.
Якщо дія сили F відбувається на покоящееся спочатку тіло масою m, то формула знаходження лінійної швидкості в будь-який момент часу t прийме вигляд:
v = a*t.
В даному випадку обидві векторні величини спрямовані в одну і ту ж сторону. Ця формула може застосовуватися для опису розгону будь-якого транспортного засобу.
Тепер припустимо, що автомобіль рухався з деякою швидкістю v0, а потім почав зупинятися. У цьому разі відповідне кинематическое рівняння прийме вид:
v = v0 + a*t.
Оскільки модуль швидкості v| авто буде зменшуватися з часом, в скалярної формі це рівність запишеться так:
v = v0 – a*t.
В даному випадку вектора швидкості і прискорення спрямовані в протилежних напрямках.
Всі формули лінійної швидкості, наведені в цьому пункті, описують прямолінійний рух з постійним прискоренням.

