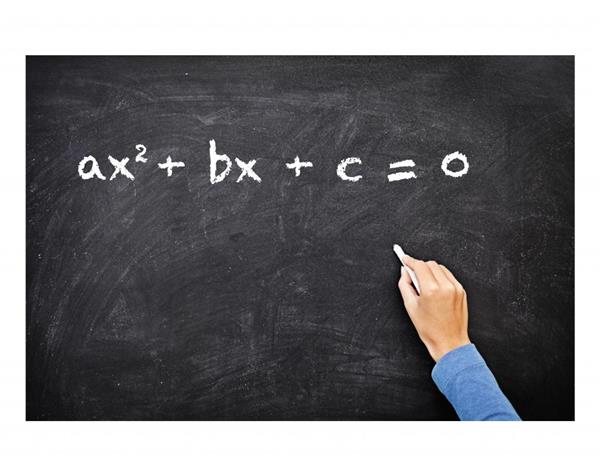Неповні квадратні рівняння являють собою окремий випадок рівностей другого порядку. Необхідно вміти вирішувати ці рівняння, оскільки вони часто зустрічаються не тільки математичних, але і у фізичних задачах. Методів їх вирішення присвячена ця стаття.
Квадратні рівняння: повні і неповні
Перед тим як розбирати способи розв’язування неповних квадратних рівнянь, слід розглянути, що вони собою представляють.
На рисунку зображено загальний вигляд рівностей другого порядку, які так називаються із-за максимального значення ступеня змінною (вона дорівнює 2), що міститься в них.
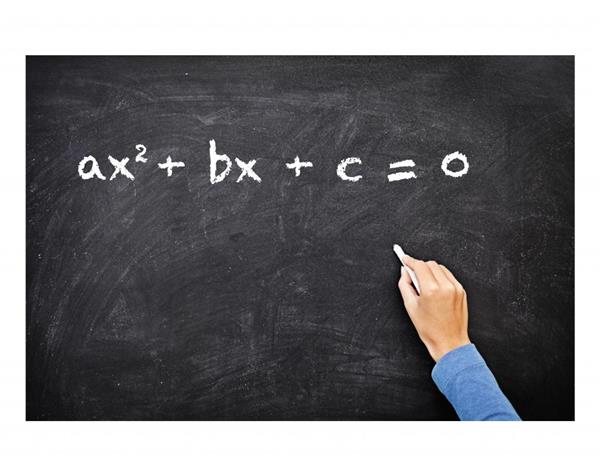
Де a, b і c – числа (коефіцієнти). Неповне рівняння виходить тоді, коли один з цих коефіцієнтів стає рівним нулю (за винятком числа a, оскільки якщо воно занулится, то рівняння перестане бути квадратним). Оскільки залишається всього три можливі комбінації нульових коефіцієнтів, то виділяють наступні типи неповних рівностей другого порядку:
- Тільки b=0. Тоді рівняння перетвориться до виду a*x2 + c = 0. Воно називається чистим, або простим неповним рівністю квадратного типу.
- Тільки c=0. Тоді отримуємо вигляд: a*x2 + b*x = 0. Воно отримало назву смешенного неповного квадратного рівняння.
- Нарешті, якщо b=0 і c=0, то ми маємо вираз a*x2=0.
Останній вид неповного рівняння не розглядається ні в одному математичному курсі, оскільки його рішення є очевидним і єдино можливим: x=0.
Можна розв’язувати неповні рівняння з допомогою формули з дискриминантом?
Так, можна, оскільки цей спосіб є універсальним для будь-яких виразів другого порядку. Однак неповні квадратні рівняння у 8 класі школи вже зустрічаються, і вони починають вивчатися раніше, ніж повні рівності цього типу, для яких вже наводиться формула з дискриминантом. Крім того, розглядуваний вид рівностей є досить простим, щоб застосовувати до них універсальні формули і виробляти ряд непотрібних обчислень.
Розглянемо прості і зрозумілі способи розв’язування неповних рівнянь другого порядку.
Рішення простого неповного рівняння
Схема його рішення в загальному випадку представлена на малюнку нижче.

Пояснимо докладніше кожен зазначений на ній крок. Насамперед необхідно привести рівняння до виду, вказаною на початку цієї схеми. Умова задачі може бути складено так, що початкове рівність буде містити більше двох доданків. Всі їх необхідно спростити (помножити, скласти і відняти) до виду чистого неповного рівності.
Після цього вільний член c переноситься в праву частину рівності і ділиться на коефіцієнт a. Для отримання невідомих x залишається взяти квадратний корінь з відношення -c/a, при цьому потрібно не забувати і враховувати, що він може бути як зі знаком мінус, так і з позитивним знаком.
Що випливає з представленої на малюнку формули? По-перше, коріння чистого неповного квадратного рівності завжди 2-а, при цьому по модулю вони обидва рівні, а по знаку відрізняються. По-друге, якщо числа c і a мають один знак, коріння x будуть уявними, якщо c і a різного знака, тоді виходять два дійсних рішення.
Рішення змішаного неповного рівняння
Для вирішення квадратного рівняння, у якого c=0, слід зробити такий самий перший крок, як і у випадку визначення коренів чистого неповного рівності, тобто привести його до виду з двома складовими: одне з них повинно містити x2, а інше x. Потім, слід застосувати метод факторизації, тобто розкласти ліву частину рівності на множники. На відміну від повного рівняння це зробити дуже просто, оскільки один із множників завжди буде іксом. Сказане вище можна записати у вигляді формули:
x*(a*x+b) = 0.
Це рівність має рішення, якщо кожен його множник є нулем. Результат обчислення коренів представлений на малюнку нижче.

Таким чином, коріння цього типу неповного рівняння завжди будуть дійсними числами, причому один з них дорівнює нулю. Знак другого кореня визначається відношенням ненульових коефіцієнтів b/a.
Приклади математичних задач
Тепер наведемо наочні приклади неповних квадратних рівнянь з рішенням.
Приклад 1. Знайдіть корені рівності 135-(2x + 3) (2x – 3) = 0. Розкриваємо дужки, отримуємо: 135-4*x2+9=0. Зауважимо, що члени, що містять x в першій мірі, скоротилися. Виконуючи перенесення вільних членів в праву частину і поділ їх на -4, отримуємо: x2 = 36. Звідки випливають два кореня: 6 -6.
Приклад 2. 23*(x2-2)=34*x-46. Як і в першому випадку, розкриваємо дужки і переносимо всі доданки в ліву частину. Маємо: 23*x2-46-34*x+46=0. Тепер скорочуємо вільні члени і розтліваємо суму на множники, отримуємо: x*(23*x-34)=0. Звідки випливає, що x=0 і x = 34/23≈1,47826.
Рішення прикладів показало, що алгоритм знаходження коренів будь-якого виду неповного рівняння другого порядку є досить простим, тому немає ніякого сенсу запам’ятовувати представлені на малюнках вище формули.
Приклад фізичної задачі
Багато школярі чули від свого вчителя фізики про те, що Галілео Галілей у XVII столітті проводив експерименти по обчисленню прискорення вільного падіння, скидаючи різні тіла з вежі в Пізі. Багатьом це здасться цікавим, але не існує жодного історичного свідчення, що такі експерименти вчений дійсно проводив. Проте в тому ж XVII столітті їх виконав інший італієць.
Джованні Річчолі – астроном і єзуїт, який дійсно зміг обчислити прискорення вільного падіння, скидаючи глиняні кулі з висоти вежі Азінеллі, що знаходиться в місті Болоньї. Річчолі отримав значення прискорення дорівнює 9,6 м/с2 (сучасна величина дорівнює 9,81 м/с2). Знаючи це число, необхідно визначити, скільки часу глиняну кулю падав на землю, враховуючи, що висота вежі дорівнює 97,6 метра.

Для вирішення завдання необхідно згадати, що шлях при рівноприскореному русі виражається формулою: l=v0*t+g*t2/2. Оскільки в момент, коли Річчолі відпускав куля, швидкість останнього була дорівнює нулю, то член v0*t = 0. Тоді ми приходимо до рівняння: 97,6 = 9,6*t2/2. Звідки отримуємо, що t = 4,51 секунди (від’ємний корінь був свідомо відкинутий).