Призма – це одна з об’ємних фігур, властивості якої вивчають у школі в курсі просторової геометрії. У цій статті розглянемо конкретну призму – шестикутну. Що це за фігура, як знайти об’єм правильної шестикутної призми і площа її поверхні? Відповіді на ці запитання містяться в статті.
Фігура призма
Припустимо, що ми маємо довільний багатокутник з числом сторін n, який знаходиться в деякій площині. До кожної вершині цього багатокутника побудуємо вектор, який не буде лежати в площині багатокутника. З допомогою цієї операції ми отримаємо n однакових векторів, вершини яких утворюють багатокутник, у точності рівний вихідному. Фігура, обмежена двома однаковими многокутниками і паралельними лініями, що з’єднують їх вершини, називається призмою.
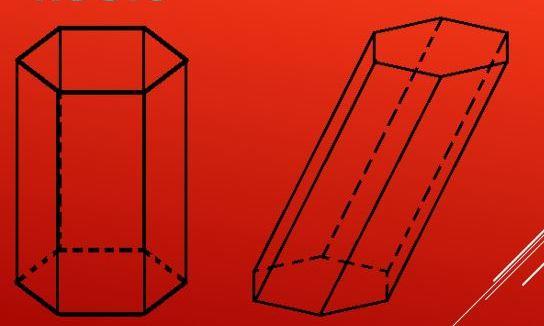
Гранями призми є дві підстави, представлені багатокутниками з n сторонами, і бічні n поверхонь-паралелограмів. Кількість ребер Р фігури пов’язане з числом її вершин і граней Р формулою Ейлера:
Р = В + Г – 2
Для багатокутника з n сторонами отримуємо n + 2 межі і 2 * n вершин. Тоді кількість ребер буде дорівнює:
Р = В + Г – 2 = 2 * n + n + 2 – 2 = 3 * n
Найпростішою призмою є трикутна, то є підставою у неї є трикутник.
Класифікація призм досить різноманітна. Так, вони можуть бути правильними і неправильними, прямокутними і косоугольными, опуклими й увігнутими.
Шестикутна призма
Ця стаття присвячена питанню обсягу правильної шестикутної призми. Спочатку познайомимося ближче з цією фігурою.
Як випливає з назви, основу шестикутної призми є гратки з шістьма сторонами і шістьма кутами. В загальному випадку таких багатокутників можна скласти безліч, однак для практики, і для розв’язання геометричних задач важливий один єдиний випадок – правильний шестикутник. У нього всі сторони рівні між собою, а кожен з 6 кутів становить 120 o. Побудувати цей багатокутник можна легко, якщо розділити коло на 6 рівних частин трьома діаметрами (вони повинні перетинатися під кутами 60 o).
Правильна шестикутна призма передбачає не тільки наявність правильного багатокутника в її основі, але і той факт, що всі бічні сторони фігури повинні бути прямими. Це можливо тільки у випадку, якщо бічні грані будуть перпендикулярні шестикутним підстав.
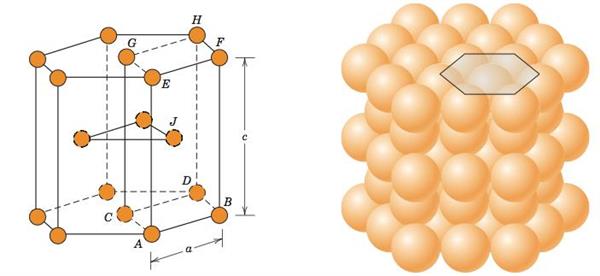
Правильна шестикутна призма – це досить досконала фігура, яка зустрічається в побуті і природі. Варто лише згадати про формі бджолиних сот або про шестигранному гайковому ключі. В області нанотехнологій також часто зустрічаються шестикутні призми. Наприклад, кристалічні решітки ГПУ і C32, які реалізуються за певних умов у титані та цирконії, а також решітка графіту мають форму шестикутних призм.

Площа поверхні шестикутної призми
Перейдемо тепер безпосередньо до питання обчислення площі та об’єму призми. Спочатку розрахуємо площу поверхні цієї фігури.
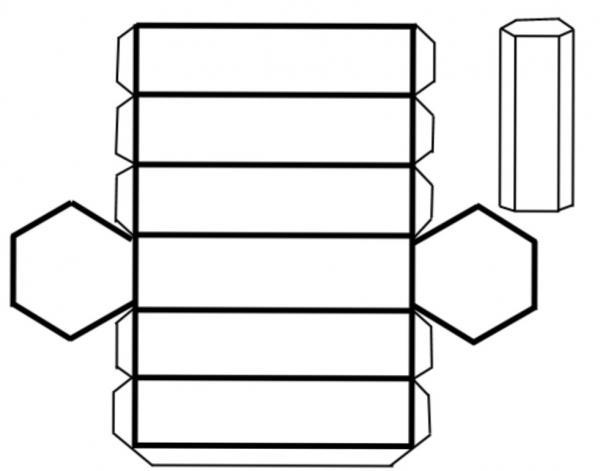
Площа поверхні будь призми обчислюється за допомогою наступного рівності:
S = 2 * So + Sb
Тобто шукана площа S дорівнює сумі площ двох підстав So та площі бічної поверхні Sb. Для визначення величини So можна зробити двома способами:
- Обчислити її самостійно. Для цього шестикутник розбивається на 6 рівносторонніх трикутників. Знаючи, що площа одного трикутника дорівнює половині добутку висоти на підставу (довжину сторони шестикутника) можна знайти площу розглянутого багатокутника.
- Скористатися відомою формулою. Вона наведена нижче:
Sn = n / 4 * a2 * ctg(pi / n)
Тут a – довжина сторони правильного багатокутника, що має n вершин.
Очевидно, що обидва способи приводять до одного результату. Для правильного шестикутника площа дорівнює:
So = S6 = 3 * √3 * a2 / 2
Площа бічної поверхні знайти просто, для цього слід помножити основу кожного прямокутника a на висоту призми h, отримане значення помножити на число таких прямокутників, тобто на 6. В результаті:
Sb = 6 * a * h
Користуючись формулою для повної площі поверхні, для правильної шестикутної призми отримуємо:
S = 3 * √3 * a2 + 6 * a * h = 3 * a * (√3 * a + 2 * h)
Як знайти об’єм призми?
Обсяг – це фізична величина, яка відображає область простору, займану об’єктом. Для призми розрахувати цю величину можна за наступною формулою:
V = So * h
Цей вираз дає відповідь на питання про те, як знайти об’єм призми довільної форми, тобто необхідно площа підстави So помножити на висоту фігури h (відстань між підставами).
Зауважимо, що наведене вираз справедливо для будь призми, включаючи увігнуті і косокутні фігури, утворені правильними многокутниками в підставі.
Формула об’єму призми правильної шестикутної
На даний момент ми розглянули всі необхідні теоретичні викладки, щоб отримати вираз для обсягу даної призми. Для цього достатньо площа підстави помножити на довжину бічного ребра, яка є висотою фігури. У результаті формула обсягу шестикутної призми прийме вигляд:
V = 3 * √3 * a2 * h / 2
Таким чином, розрахунок обсягу розглянутої призми передбачає знання всього двох величин: довжини сторони її основи та висоти. Ці дві величини однозначно визначають обсяг фігури.
Порівняння обсягів шестикутної призми і циліндра

Вище було сказано, що підстава шестикутної призми може бути легко побудовано з використанням колу. Також відомо, що якщо збільшувати кількість сторін правильного многокутника, то його форма буде наближатися до кола. У зв’язку з цим представляє інтерес розрахувати, на скільки обсяг правильної шестикутної призми відрізняється від цього значення для циліндра.
Для відповіді на поставлене питання необхідно обчислити довжину сторони шестикутника, вписаного в окружність. Можна легко показати, що вона дорівнює радіусу. Позначимо радіус окружності буквою R. Припустимо, що висота циліндра і призми дорівнює деякому значенню h. Тоді об’єм призми дорівнює наступного значення:
Vp = 3 * √3 * R2 * h / 2
Об’єм циліндра визначається за тією ж формулою, що і обсяг для довільної призми. Враховуючи, що площа кола дорівнює pi * R2, обсягу циліндра маємо:
V = pi * R2 * h
Знайдемо відношення обсягів цих фігур:
Vp / V = 3 * √3 * R2 * h / 2 / (pi * R2 * h) = 3 * √3 / (2 * pi)
Число “пі” дорівнює 3,1416. Підставляючи його, отримуємо:
Vp / V = 0,827
Таким чином, обсяг правильної шестикутної призми становить близько 83 % від обсягу циліндра, в який вона вписана.

