Розгляд в геометрії прямих і площин передбачає вивчення питання їх взаємного розташування. У цій статті дамо визначення перпендикуляра і похилої площини та прямої, а також розглянемо властивості, якими вони володіють.
Рівняння для площини і прямої
До розгляду питання перпендикуляра і похилої до різних геометричних об’єктів не можна переходити, поки не вивчені математичні способи задавання цих об’єктів. Мова йде про види рівнянь площини і прямої.
Пряма в просторі, двовимірному і тривимірному, часто задається у вигляді векторного рівняння. Воно має форму:
(x; y; z) = (x0; y0; z0) + λ*(a; b; c)
У перших дужках правої частини рівності стоять координати точки, що належить прямій. У других дужках знаходяться координати вектора, що є направляючим для даного геометричного об’єкта. Параметр λ може приймати довільне значення.
З даним рівнянням легко працювати в тривимірному випадку. У двовимірному випадку воно також може бути використане (тільки без координати z). Проте в координатній площині пряма задається часто в іншому вигляді:
A*x + B*y + C = 0
Тут A, B, C – деякі числа, причому (A; B) – це вектор, який перпендикулярний прямій. Це рівняння називається загальним.
Площина як двовимірний об’єкт в просторі найчастіше задається у загальному вигляді, тобто:
A*x + B*y + C*z + D = 0
Важливо не плутати це рівняння з попереднім. Тут вектор, який задається координатами (A; B; C), виявляється нормальним (перпендикулярним до площини, тобто є її напрямним вектором.
Перпендикуляр для прямої і для площині
Вивчення питання похилій і перпендикуляра до прямої і площини почнемо з перпендикулярного вектора. Вище вже було сказано, що для прямої на площині і для площини в тривимірному просторі, які задані у вигляді рівняння загального виду, визначити координати перпендикулярного вектора не становить праці. Головною його властивістю, яке випливає з визначення перпендикуляра, є те, що він з даним геометричним об’єктом складає кут 90o.
Синій відрізок на малюнку нижче є перпендикуляром до зображеної прямій.

Ще однією властивістю перпендикуляра до прямої є те, що його скалярний твір з напрямним вектором буде дорівнює нулю.
Перпендикуляр до площини, який представлений вектором і прямий, показаний на малюнку нижче.
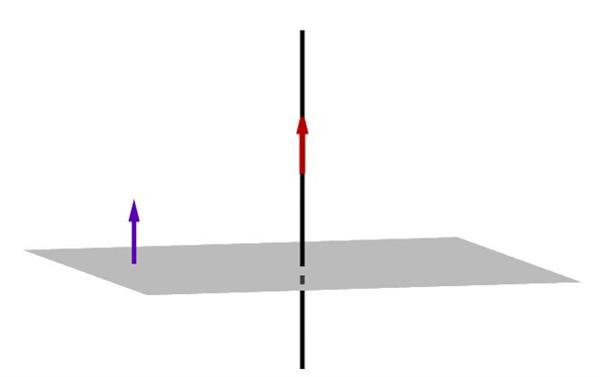
Так само, як і у випадку з прямою, скалярний добуток цього перпендикуляра на будь-який вектор, що належить площині, буде дорівнює нулю.
Якщо для площини перпендикуляр не відомий, то знайти його нескладно. Для цього необхідно обчислити векторний добуток будь-яких двох паралельних векторів, що належать площині.
Знаходження перпендикуляра до площини і прямої важливо, оскільки дозволяє обчислити відстань від зазначених об’єктів до деякій точці простору.
Похила до прямої
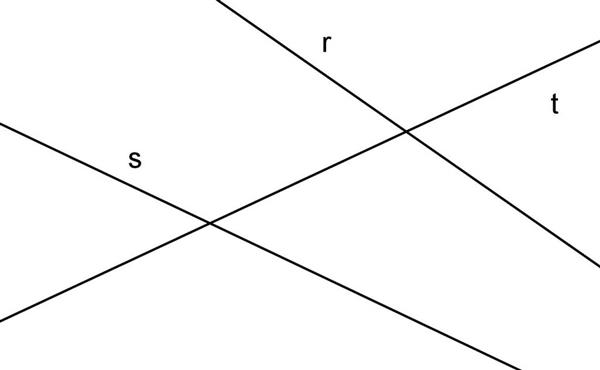
Продовжуємо розглядати властивості перпендикуляра і похилої до прямої і площини. Дамо спочатку визначення похилій для прямої. Під нею розуміють будь-яку пряму, що перетинає дану під деяким кутом, не рівним 90 o.
Якщо з деякої точки похилій прямій опустити перпендикуляр на іншу пряму, відрізок, утворений точкою перпендикуляра і точкою перетину об’єктів, буде проекцією відрізка похилій на пряму.
Розрахувати кут φ між пересічними прямими досить просто. Для цього користуються такою формулою:
φ = arccos(|(v*u)|/(|v|*|u|))
Тут v і u – це напрямні вектори розглянутих прямих.
Для випадку на площині цією формулою можна користуватися завжди без попередніх обчислень. У просторі слід враховувати, що прямі можуть утворювати певний кут між собою, але при цьому не перетинатися (бути мимобіжними). У такому випадку спочатку слід перевірити, чи мають прямі спільну точку перетину.
Похила до площини
У питанні перпендикуляра і похилої залишається розглянути похилу до площини.
Будь-яка пряма, яка перетинає задану площину під деяким гострим кутом, є похилій до неї. Якщо кожну точку прямої проектувати на площину, провівши відповідні перпендикуляри до неї, то ми отримаємо проекцію всій прямій. Кут між проекцією і вихідної прямої є кутом перетину розглянутих об’єктів.
Нижче на малюнку наводиться пряма r, яка є похилій площині «пі».
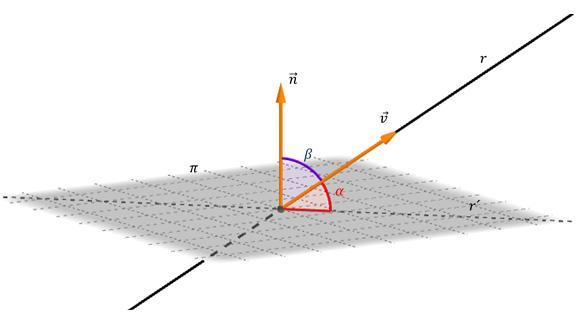
Пряма r’ – це проекція r. Кут між «пі» і r позначено як α. Для його визначення користуються наступною формулою:
α = arcsin(|(v*n)|/(|v|*|n|))
Де v і n – направляючі вектори прямої r і площини «пі» відповідно (див. рис.).
Приклад завдання
Покажемо, як можна використовувати отримані знання про перпендикулярі і похилою, щоб вирішити наступну задачу:
Дано рівняння прямої та площини:
(x; y; z) = (1; 0; 2) + λ*(1; 1; 1);
x + 2*y – 1 = 0
Задана пряма є похилій площині. Необхідно визначити, під яким кутом вони перетинаються.
Випишемо координати відповідних направляючих векторів:
для прямої: v = (1; 1; 1);
для площині: n = (1; 2; 0)
Підставимо ці значення в формулу для кута α, отримуємо:
α = arcsin(|((1; 1; 1)*(1; 2; 0))|/(|(1; 2; 0)|*|(1; 1; 1)|)) =
= arcsin(3/(√5*√3)) ≈ 50,77 o
Таким чином, пряма, будучи похилій площині, перетинає її під кутом 50,77 o.

