Коли вивчають механічний рух у фізиці, то після ознайомлення з рівномірним і рівноприскореним переміщенням об’єктів, переходять до розгляду руху тіла під кутом до горизонту. В даній статті розглянемо докладніше це питання.
Що собою представляє рух тіла під кутом до горизонту?
Цей тип переміщення об’єктів виникає, коли людина кидає камінь в повітря, гармата здійснює постріл ядром, або воротар вибиває від воріт футбольний м’яч. Всі подібні випадки розглядаються наукою баллистикой.
Зазначений вид переміщення об’єктів у повітрі відбувається по параболічної траєкторії. В загальному випадку проведення відповідних розрахунків є справою не простим, оскільки необхідно враховувати опір повітря, обертання тіла під час польоту, обертання Землі навколо осі і деякі інші фактори.
У даній статті ми не будемо враховувати всі ці фактори, а розглянемо питання з суто теоретичної точки зору. Тим не менш, отримані формули досить добре описують траєкторії тіл, що пересуваються на невеликі відстані.
Отримання формул для розглянутого виду руху

Виведемо формули руху тіла до горизонту під кутом. При цьому будемо враховувати тільки одну-єдину силу, діючу на летить об’єкт – силу тяжіння. Оскільки вона діє вертикально вниз (паралельно осі y і проти неї), то, розглядаючи горизонтальну і вертикальну складові руху, можна сказати, що перша буде мати характер рівномірного прямолінійного переміщення. А друга – равнозамедленного (равноускоренного) прямолінійного переміщення з прискоренням g. Тобто, компоненти швидкості через значення v0 (початкова швидкість) і θ (кут напрямку руху тіла) запишуться так:
vx = v0*cos(θ)
vy = v0*sin(θ)-g*t
Перша формула (vx) справедлива завжди. Що стосується другого, то тут потрібно відзначити один нюанс: знак мінус перед твором g*t ставиться тільки в тому випадку, якщо вертикальна компонента v0*sin(θ) спрямована вгору. В більшості випадків так і відбувається, однак, якщо кинути тіло з висоти, направивши його вниз, тоді у виразі для vy слід поставити знак “+” перед g*t.
Проинтегрировав формули для компонент швидкості за часом, і враховуючи початкову висоту h польоту тіла, отримуємо рівняння для координат:
x = v0*cos(θ)*t
y = h+v0*sin(θ)*t-g*t2/2
Обчислення дальності польоту
При розгляді у фізиці руху тіла до горизонту під кутом, корисним для практичного застосування, виявляється розрахунок дальності польоту. Визначимо її.
Оскільки це переміщення являє собою рівномірний руху без прискорення, то досить підставити в нього час польоту і отримати необхідний результат. Дальність польоту визначається виключно переміщенням вздовж осі x (паралельно горизонту).
Час перебування тіла в повітрі можна обчислити, прирівнявши до нуля координату y. Маємо:
0 = h+v0*sin(θ)*t-g*t2/2
Це квадратне рівняння вирішуємо через дискриминант, отримуємо:
D = b2 – 4*a*c = v02*sin2(θ) – 4*(-g/2)*h = v02*sin2(θ) + 2*g*h,
t = (-b±√D)/(2*a) = (-v0*sin(θ)±√(v02*sin2(θ) + 2*g*h))/(-2*g/2) =
= (v0*sin(θ)+√(v02*sin2(θ) + 2*g*h))/g.
В останньому виразі один корінь зі знаком мінуса відкинутий, на увазі його незначного фізичного значення. Підставивши час польоту t вираз для x, отримуємо дальність польоту l:
l = x = v0*cos(θ)*(v0*sin(θ)+√(v02*sin2(θ) + 2*g*h))/g.
Простіше всього це вираз проаналізувати, якщо початкова висота дорівнює нулю (h=0), тоді отримаємо просту формулу:
l = v 02*sin(2*θ)/g
Цей вираз свідчить, що максимальну дальність польоту можна отримати, якщо тіло кинути під кутом 45o (sin(2*45 o) = м1).
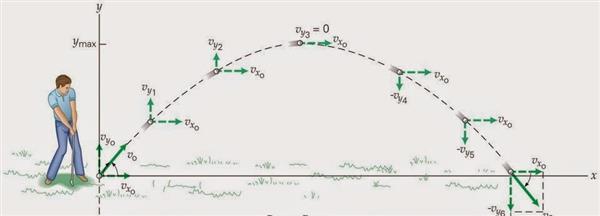
Максимальна висота підйому тіла
Крім дальності польоту, також корисно знайти висоту над землею, на яку може піднятися тіло. Оскільки цей тип руху описується параболою, гілки якої спрямовані вниз, то максимальна висота підйому є її екстремумом. Останній розраховується шляхом рішення рівняння для похідної по t y:
dy/dt = d(h+v0*sin(θ)*t-g*t2/2)/dt = v0*sin(θ)-gt=0 =>
=> t = v0*sin(θ)/g.
Підставляємо цей час в рівняння y, отримуємо:
y = h+v0*sin(θ)*v0*sin(θ)/g-g*(v0*sin(θ)/g)2/2 = h + v02*sin2(θ)/(2*g).
Цей вираз свідчить, що на максимальну висоту підніметься тіло, якщо його кинути вертикально вгору (sin2(90 o) = 1).

