Коли вирішують будь-які завдання з фізики, в яких є рухомі об’єкти, то завжди говорять про сили тертя. Їх враховують, або ними нехтує, але факт їх присутності ні в кого не викликає сумніву. У цій статті розглянемо, що таке момент сил тертя, а також наведемо проблеми, для усунення яких скористаємося отриманими знаннями.
Сила тертя та її природа
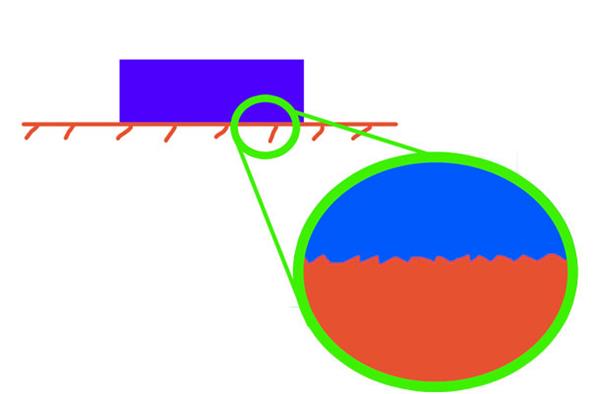
Кожен розуміє, що якщо одне тіло рухається по поверхні іншого абсолютно будь-яким способом (ковзає, котиться), то завжди існує деяка сила, яка перешкоджає цьому переміщенню. Вона називається динамічною силою тертя. Причина її виникнення пов’язана з тим фактом, що будь-які тіла мають мікроскопічні шорсткості на своїх поверхнях. Коли стикаються два об’єкти, то їх шорсткості починають взаємодіяти один з одним. Ця взаємодія носить як механічний характер (пік потрапляє в западину), так і відбувається на рівні атомів (дипольні тяжіння, ван-дер-ваальсовые та інші).
Коли дотичні тіла перебувають у спокої, то, щоб привести їх у рух один відносно одного, необхідно докласти зусилля, яке більше такого для підтримки ковзання цих тіл одне щодо одного з постійною швидкістю. Тому крім динамічної також розглядають статичну силу тертя.

