Прочитавши цю статтю, ви дізнаєтеся, як знайти висоту конуса. Наведений у ній матеріал допоможе глибше розібратися в питанні, а формули виявляться дуже корисними у вирішенні завдань. У тексті розібрані всі необхідні базові поняття і властивості, які обов’язково стануть в нагоді на практиці.
Фундаментальна теорія
Перед тим, як знайти висоту конуса, необхідно розібратися з теорією.
Конус – фігура, яка плавно звужується від плоского підстави (часто, хоча і необов’язково, кругового) до точки, званої вершиною.
Конус формується набором відрізків, променів або прямих, що з’єднують спільну точку з підставою. Останнє може обмежуватися не лише колом, але і еліпсом, параболою або гіперболою.
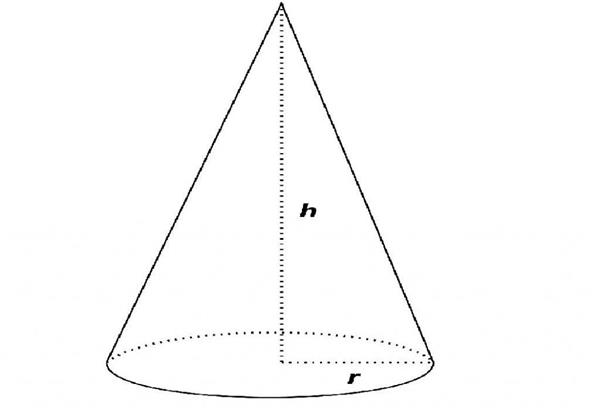
Вісь – це пряма (якщо така є), навколо якої фігура має кругову симетрію. Якщо кут між віссю і основою становить дев’яносто градусів, то конус прийнято називати прямим. Саме така варіація найчастіше зустрічається в задачах.
Якщо в основі лежить багатокутник, то об’єкт є пірамідою.
Відрізок, що з’єднує вершину і лінію, що обмежує основу, називають утворюючої.
Як знайти висоту конуса
Підійдемо до питання з іншого боку. Для початку використовуємо обсяг конуса. Щоб його знайти треба обчислити добуток висоти з третьою частиною площі.
V = 1/3 × S × h.
Очевидно, що з цього можна отримати формулу висоти конуса. Досить лише зробити правильні алгебраїчні перетворення. Розділимо обидві частини рівності на S і помножимо на трійку. Отримаємо:
h = 3 × V × 1/S.
Тепер ви знаєте, як знайти висоту конуса. Однак для вирішення завдань вам можуть знадобитися й інші знання.
Важливі формули і властивості
Наведений нижче матеріал однозначно допоможе вам у вирішенні конкретних завдань.
Центр маси тіла знаходиться на четвертій частині осі, починаючи від основи.
В проективної геометрії циліндр – це просто конус, вершина якого знаходиться на нескінченності.
Такі властивості працюють тільки для прямого кругового конуса.
- Дані радіус основи r і висота h, тоді формула для площі буде виглядати так: П × r2. Відповідно зміниться і остаточне рівняння. V = 1/3 × Д × r2 × h.
- Обчислити площу бічної поверхні можна перемноживши число “пі”, радіус і довжину твірної. S = П × r × l.
- Перетин довільної площини з фігурою є одним з конічних перерізів.
Часто зустрічаються задачі, де необхідно використати формулу для об’єму зрізаного конуса. Вона виводиться із звичайної і має такий вигляд:
V = 1/3 × Д × h × (R2 + Rr + r2), де: r -радіус нижньої основи, R – верхнього.
Всього цього буде цілком достатньо для рішення різноманітних прикладів. Хіба що можуть знадобитися знання, не пов’язані з цією темою, наприклад, властивості кутів, теорема Піфагора та інше.
