Існують кілька способів розв’язування квадратних рівнянь, однак використання формули, яка пов’язує коефіцієнти рівностей названого типу, є універсальним. Цей спосіб часто називають методом “через дискриминант”. Приклади розв’язання квадратних рівнянь з допомогою нього наводяться в даній статті. Про них має знати кожен старшокласник.
Квадратні рівняння
Приклади з дискриминантом ставляться до вирішення квадратних рівнянь. Такі рівняння мають вигляд, представлений на фото нижче.
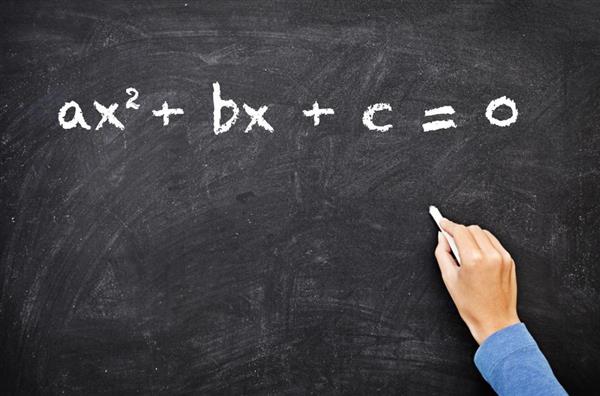
Тут a, b і c – деякі коефіцієнти (числа), які називаються квадратичним, лінійним і вільним членом, відповідно. Якщо відомі значення ікса такі, при яких рівність на фото є істиною, тоді говорять про те, що вони є коренями цього рівняння.
Як можна помітити, це рівняння називається квадратним, бо “2” є максимальним ступенем, до якої зводиться x. Якщо a = 0, тоді рівняння перетворюється в лінійне.
Оскільки максимальна ступінь рівняння дорівнює двом, то можуть існувати лише 0, 1 або 2 його кореня, які будуть приймати дійсні числові значення.
Щоб вирішити назване рівняння, можна скористатися кількома методами. Тим не менш, самим простим і надійним з них є застосування формули з дискриминантом.
Якою формулою слід користуватися?
Формула методу розв’язання квадратних рівнянь через дискриминант записується так, як представлено на малюнку нижче.
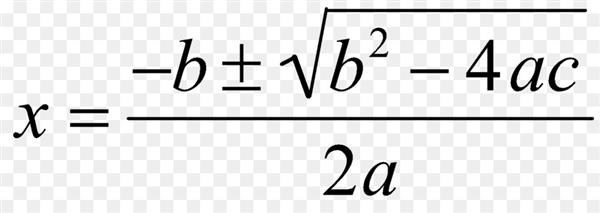
Можна бачити, що для її використання необхідно знання всіх трьох коефіцієнтів рівняння, а знак “±”, що стоїть перед коренем, говорить про те, що формула дозволяє знаходити одночасно два різних кореня.
Підкореневий вираз називається дискриминантом. Він зазвичай позначається латинською буквою D або грецької Δ. Чому виділяють саме цю частину представленої формулою? Справа в тому, що від знака D залежить, скільки коренів буде мати відповідне рівняння, якими вони будуть.
Так, якщо D позитивний, то вираз призводить до двом різним рішенням квадратного рівняння, якщо ж D негативний, тоді немає дійсних чисел, які б задовольняли початкового рівності. У цьому випадку говорять про уявні корені, виражених у вигляді комплексних чисел. Нарешті, якщо D = 0, то формула призводить до існування одного єдиного кореня.

Важливі властивості коренів у методі “через дискриминант”
Перш ніж перейти до розгляду конкретних прикладів рівнянь з дискриминантом, необхідно привести два важливих властивості коренів, отриманих методом вирішення з використанням даної формули.
Перша властивість полягає в тому, що їх сума (x1 + x2) дорівнює відношенню лінійного коефіцієнта (b) до першого або квадратичним коефіцієнту (a), взяте з протилежним знаком, тобто -b/a.
Друга властивість полягає в тому, що твір x1 * x2 завжди дорівнює відношенню вільного члена (c) до першого коефіцієнту (a), тобто c / a.
Наведені рівності, які пов’язують корені рівняння за його коефіцієнтами, що складають суть так званої теореми Вієта.
Зазначимо, що ці формули справедливі для будь-якого рівняння квадратного (в тому числі і неповного, тобто у якого b і c дорівнює нулю).
Далі в статті розглянемо використання формули з дискриминантом квадратного рівняння у прикладах, які будуть сформульовані у вигляді задач, що мають практичне значення.
Завдання № 1. Добуток і сума чисел
Першим прикладом рівняння з дискриминантом буде наступний: необхідно назвати два числа, сума яких дорівнює 34, а твір 273.
Згідно з умовою задачі, складемо систему рівнянь, позначивши невідомих два числа, як x1 і x2. Отримуємо:
x1 + x2 = 34
x1 * x2 = 273.
Висловивши x2 через x1 у першому рівнянні, і підставивши його в друге, маємо: (34 -x1) * x1 = 273. Розкриваючи дужки, отримаємо: (x1)2 – 34 * x1 + 273 = 0. Тобто умова завдання звелося до вирішення квадратного рівняння.
Вирішуємо цей приклад формулою з дискриминантом: D = (-34)2 – 4 * 1 * 273 = 64. Вийшло зручне для обчислення квадратного кореня числа. Рішення цього рівняння будуть мати вигляд: x1 = (34 ± √64) / 2 = (21; 13). Кожне з отриманих чисел x1 підставимо в перше рівняння наведеної вище системи, отримуємо: x2 = (34 – 21 = 13; 34 – 13 = 21).
Таким чином, всього одна пара чисел (13 і 21) задовольняє умові задачі. Оскільки суму ми вже перевірили, то перевіримо тепер твір: 13 * 21 = 273.
Завдання №2. Складання та розв’язання рівняння по заданому умові
У наведеному далі прикладі формула з дискриминантом також знадобиться для його розв’язання. Отже, умова формулюється наступним чином: знайти число, подвійний квадрат якого перевершує його на 45. Записуємо мовою математики це умова: 2 * x2 – x = 45. Тобто знову задача зводиться до знаходження невідомого x в квадратному рівнянні.
Перенесемо всі члени в ліву частину рівності і обчислимо дискриминант: D = 1 – 4 * 2 * (-45) = 361. Корінь цього числа дорівнює 19. Тому рішеннями рівняння будуть числа: x = (1 ± 19) / (2 * 2) = (5; -4,5).
Перевіримо цей результат: 2 * 52 = 50, що дійсно перевершує число 5 на 45; 2 * (-4,5)2 = 40,5, це число також задовольняє умові (40,5 – (-4,5) = 45).
Завдання №3. Визначення сторін прямокутного трикутника

Ще одним прикладом з дискриминантом квадратного рівняння є наступна задача: відомо, що різниця між двома сторонами прямокутника дорівнює 70 див. Необхідно знайти його боку, якщо діагональ фігури дорівнює 130 див.
Умова задачі дозволяє скласти систему з двох рівнянь:
x1 – x2 = 70
(x1)2 + (x2)2 = 1302.
Тут x1 і x2 – невідомі сторони прямокутника. Пояснимо, звідки взялося друге рівняння. Оскільки діагональ прямокутника утворює з двома його сторонами трикутник з кутом 90 o, то сторони, які дорівнюють x1 і x2, є катетами, тому можна скористатися їх зв’язком з діагоналлю -гіпотенузою (теорема Піфагора).
Висловивши з першого рівняння x2, підставивши її значення у друге рівняння, розкривши в ньому дужки, отримуємо: 2 * (x1)2 – 140 * x1 – 12 000 = 0. Вирішуємо це класичне рівняння квадратне: D = (140)2 – 4 * 2 * (-12 000) = 115600. Використання калькулятора дозволяє розрахувати корінь з цього числа, він дорівнює 340. Корені цього рівняння рівні: x1 = (140 ± 340) / 4 = (120; -50). Від’ємне число слід відразу відкинути, оскільки сторона прямокутника – позитивна величина.
Підставляючи x1 = 120 см в перше рівняння системи, отримуємо, що x2 = 50 див.
Таким чином, невідомі сторони прямокутника дорівнюють 120 см і 50 см
Завдання №4. Два мотоцикліста

Наступний приклад рівняння через дискриминант пов’язаний з вирішенням завдання про двох мотоциклістів. Відомо, що кожен з них виїхав назустріч іншому. Початкова відстань між ними було одно 130 км, швидкість одного становила 30 км/год, а інший їхав зі швидкістю на 33 км/год більше, ніж число годин, через які вони зустрілися. Необхідно знайти, через який час зустрінуться мотоциклісти.
Позначимо невідоме час буквою t. З умови задачі випливає, що швидкість другого мотоцикліста дорівнювала 33 + t. До зустрічі кожен мотоцикліст проїхав відстань 30 * t і (33 + t) * t. Очевидно, що в момент зустрічі обидва транспортних засоби подолали сумарна відстань 130 км (див. умову задачі). Тоді отримуємо рівняння: 30 * t + (33 + t) * t = 130. Розкриваючи дужки, отримуємо наступний вигляд: t2 + 63 * t – 130 = 0. Обчислюємо в цьому прикладі дискриминант: D = (63)2 -4 * 1 * (-130) = 4489. Корінь з нього буде дорівнює 67. Значення t, задовольняють рівнянню, будуть рівні: t = (-63 ± 67) / 2 = (2; -65). Оскільки час не може бути від’ємним, отримуємо відповідь на завдання: мотоциклісти зустрінуться через 2 години.
Завдання №5. Оренда човна групою молодих людей

Завершити цю статтю хотілося б прикладом і рішенням через дискриминант однією цікавою завдання: кілька молодих людей вирішили орендувати човен за 14 000 рублів. Вони цю суму поділили на всіх. Однак у самий останній момент троє людей відмовилися плисти на човні, тому кожен з решти змушений був доплатити ще 1500 рублів. Скільки людей хотіли орендувати човен спочатку?
Нехай спочатку було x молодих людей. Тоді кожен з них повинен був заплатити суму 14000 / x рублів. Як тільки троє осіб відмовилися плисти, остання сума для кожного залишився стала дорівнює 14000 / (x-3). Оскільки остання сума зросла порівняно з первісною на одну людину на 1500 рублів, то можна скласти таке рівняння: 14000 / (x-3) – 14000 / x = 1500.
Наведемо це рівняння до квадратного. Маємо: 14000 * x – 14000 * x + 14000 * 3 = 1500 * x * (x-3). Розкриваючи дужки і, спрощуючи вираз, отримаємо: 1500 * x2 – 4500 * x – 42 000 = 0. Розділивши обидві частини рівності на 1500, отримаємо вираз: x2 – 3 * x – 28 = 0. Вирішуємо цей приклад дискриминантом: D = 9 – 4 * 1 * (-28) = 121. Тоді x = (3 ± 11) / 2 = (7; -4).
Таким чином, спочатку група молодих людей складалася з 7 осіб.