Геометрія – надзвичайно цікава наука, яку починають викладати в російських школах в сьомому класі. Але іноді тема, пройдена на уроці, зовсім не зрозуміла, а спроби прочитати параграф у підручнику тільки погіршують ситуацію. Тоді на допомогу приходить всезнаючий Інтернет або ж деякі учні просто відкривають готові домашні завдання, що в корені невірно, адже тоді питання залишається без відповіді, мозок не розвивається, виникають ще більші проблеми зі сприйняттям інформації на уроці, що веде до поганих оцінок. У цій статті ми розберемо один із базових елементів, за допомогою якого вирішуються дуже багато завдань. Яке визначення висоти трикутника? Як її будувати? Відповіді на ці та багато інших запитань ви знайдете в цій статті.
Визначення висоти трикутника
Розуміння суті елемента, і навіщо він потрібен, починається завжди з вивчення теорії. Так, висота трикутника – перпендикуляр, опущений з вершини трикутника на пряму, що містить протилежну сторону. Чому не на саму сторону? З цим ми розберемося трохи пізніше.
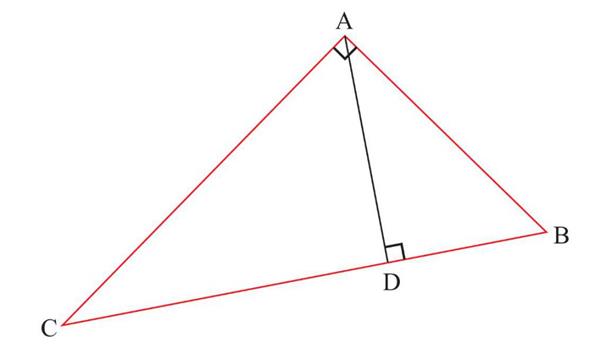
Скільки можна провести висот у трикутнику? Кількість висот збігається з кількістю вершин, тобто три. Всі три перетину перпендикулярів трикутника перетинаються в одній точці.
Давайте також повторимо теорію про двох інших важливих елементах – бісектрисі і медіаною.
Бісектриса – промінь, що з’єднує вершину трикутника з протилежною стороною, при цьому поділяючи кут на дві рівні частини.
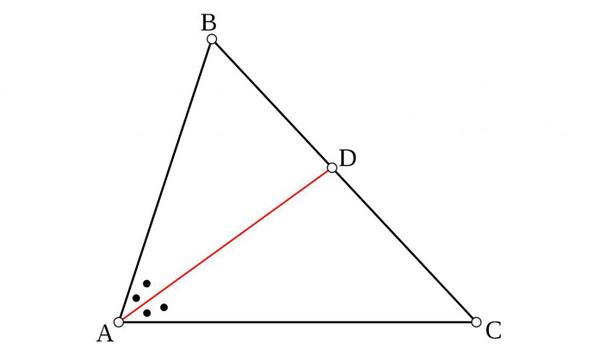
Медіана – відрізок, що з’єднує вершину кута з серединою протилежної сторони.
Типи трикутників
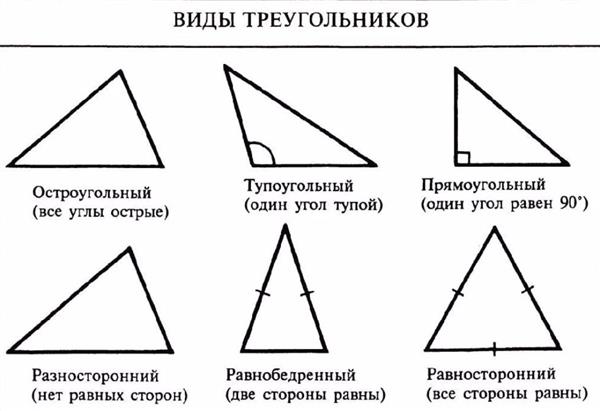
Різновидів трикутники в геометрії дуже багато, в кожному з них висоти грають свою роль. Давайте розглянемо детально всі типи цієї фігури. Визначення висоти трикутника допоможе нам у цьому.
Почнемо з звичайного гострокутного різнобічного трикутника, у якого всі кути гострі і не рівні 60 градусів, а сторони не рівні один одному. У цій геометричній фігурі висоти перетнуться, але ця точка не буде центром трикутника.
У тупоугольном трикутнику градусна міра одного кута 90 градусів. Висоту, що виходить з тупого кута, опускають на пряму, що містить протилежну сторону.
Наступним буде рівнобедрений трикутник. У нього рівні тільки дві сторони і два кути при основі. Цікаво те, що висота, проведена з вершини до основи трикутника, збігається з медіаною та бісектрисою.
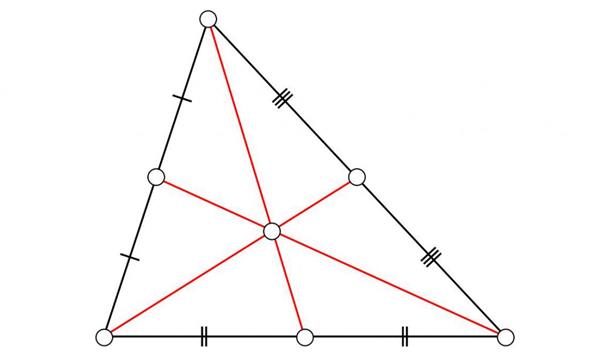
У рівносторонньому трикутнику рівні всі сторони і кути, які дорівнюють 60 градусів (кожен). Всі висоти, медіани і бісектриси збігаються і перетинаються в одній точці – центрі трикутника.
Стандартні формули, пов’язані з висотою
Для кожного з перерахованих випадків є формули для визначення висоти, але в цьому пункті ми розглянемо лише ті, що підходять для кожного типу трикутника. Таких формул чотири.
- Найбільш проста і доступна: H = 2S/a. Знаючи площу і довжину сторони, до якої опущено перпендикуляр, ми можемо знайти висоту, розділивши подвійне твір площі на бік.
- Якщо трикутник укладений в коло, то і на цей випадок є формула: H = bc/2R. Для знаходження висоти, потрібно сторони, на які не падає перпендикуляр, розділити на подвійне твір радіусу описаного навколо трикутника кола.
- Знаючи тільки боку, ми також можемо знайти висоту H = (2√(p(p-a)*(p-b)*(p-c)))/a, де: p – півпериметр; a – сторона, на яку опущена висота; b, c – сторони, на які не падає перпендикуляр.
- А для тих, хто знає вже почав проходити тригонометрію і знає, що таке синус і косинус, існує така формула: H = bsinY = csinB. Синус – відношення противолежащей сторони до перпендикуляру; H – перпендикуляр; b і c – сторони, противолежащие кутах Y і B відповідно.
Прямокутний трикутник
Ви могли подумати, що ми забули про прямокутних трикутниках, але це не так. Прямокутний трикутник – трикутник, у якого один з кутів дорівнює 90 градусів. Висота в прямокутному трикутнику тільки одна, адже дві останні є сторонами, а точніше катетами. Єдиний перпендикуляр виходить з прямого кута і опускається на гіпотенузу. Формули для знаходження для цього випадку досить багато:
- H = ab/c;
- H = ab/√(a2 +b 2);
- H = csinAcosA=c sinBcosB;
- H = bsinA=a sinB;
- H = √de.
де:
H – висота;
a, b – катети;
с – гіпотенуза;
A, B – кути при гіпотенузі;
d, e – відрізки, отримані від ділення гіпотенузи заввишки.
Висновок
Так, у цій статті ми розглянули визначення висоти трикутника. Які є типи трикутників? Які формули можна використовувати для знаходження висоти? Тепер на всі ці питання ви зможете дати розгорнуті, а головне правильні відповіді.

