Додекаедр – це об’ємна геометрична фігура, яка має 12 граней. Це основна його характеристика, оскільки кількість вершин і кількість ребер можуть бути змінені. Розглянемо у статті властивості цієї фігури, її використання в даний час, а також деякі цікаві історичні факти, пов’язані з нею.
Загальні поняття про фігуру
Додекаедр – це слово взято з мови стародавніх греків, що буквально означає “фігура з 12-ю гранями”. Його грані являють собою багатокутники. Враховуючи властивості простору, а також визначення додекаедр, можна сказати, що його багатокутники можуть мати 11 сторін і менше. Якщо межі фігури утворені правильними пентагонами (багатокутник, має 5 сторін і 5 вершин), то такий додекаедр називається правильним, він входить в число 5-ти платонівських об’єктів.
Геометричні властивості правильного додекаедр
Розглянувши питання про те, що таке додекаедр, можна перейти до характеристики основних властивостей правильної об’ємної фігури, тобто утвореної однаковими пятиугольниками.
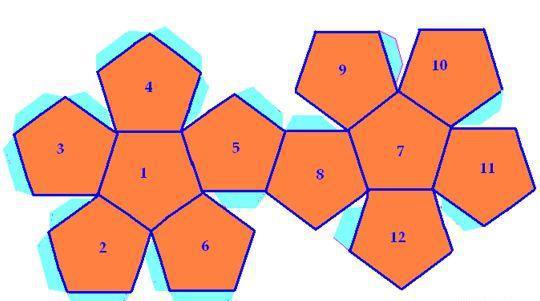
Оскільки розглянута фігура є об’ємною, опуклою і складається з багатокутників (пентагонов), то для неї справедливо правило Ейлера, яке встановлює однозначну залежність між числом граней, ребер і вершин. Воно записується у вигляді: Р + В = Р + 2, де Р – кількість граней, вершин, Р – ребер. Знаючи, що правильний додекаедр – це дванадцятигранник, число вершин якого складає 20, то, використовуючи правило Ейлера, отримуємо: Р = Р + У – 2 = 30 ребер. Кути між сусідніми гранями цієї платонівської фігури є однаковими, вони рівні 116,57 o.

