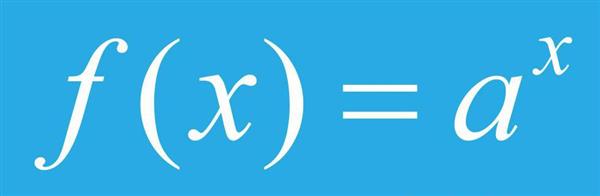Експоненціальна залежність являє собою математичну функцію, яка є корисною для опису процесу, де швидко збільшується або швидко зменшується кількість яких-небудь елементів. Існує безліч прикладів використання цієї залежності в біології, фізиці, економіці, медицині та інших сферах людської діяльності.
Визначення експоненційної залежності
Для того щоб розуміти, що означають слова “ця кількість зростає експоненціально” або “цей процес характеризується експоненціальним спадом”, необхідно розглянути поняття самої експоненційної функції. Для цього візьмемо деяке додатне число “a”, яке не дорівнює 1, і піднесемо його до степеня “x”, при цьому x-змінна може мати як позитивні, так і негативні значення, але не повинна дорівнювати нулю. Також візьмемо деяке постійне число k (константа), яке не дорівнює нулю. Тепер введемо математичну функцію f(x) = k*ax. Зведення в ступінь “x” позитивного числа “a” – це експоненціальна залежність, а сама функція f(x) називається показовою. У функції f(x) число a називається підставою, а “x” – це незалежна змінна.
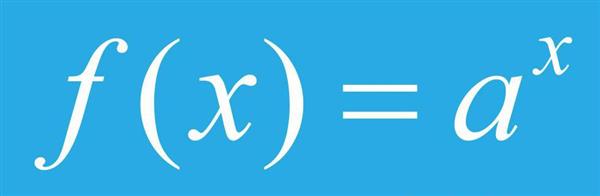
Відзначимо, що в математиці часто фігурує підстава експоненційної функції “a”, яке приблизно дорівнює 2,718. Це число позначається латинською буквою “e” і називається числом Ейлера. Зазначене число відіграє важливу роль в математичній теорії меж, а також у багатьох фізичних процесах в природі, наприклад, тиск повітря з висотою на нашій планеті зменшується за експоненціальним законом, у функціональній залежності якого підставою виступає число Ейлера.
Графік експоненційної залежності
Розглянемо властивості експоненційної функції y = ax, для цього звернемося до графіка, представленого вище. Першим важливим властивістю є те, що яким би підставою “a” не була представлена функція, вона завжди буде проходити через точку з координатами (0,1), оскільки a0 = 1.
З графіка експоненційної залежності також видно, що функція ax для будь-яких значень змінної x” приймає тільки позитивні значення. При великих негативних значеннях “x” функція швидко наближається до осі абсцис, тобто прагне до нуля. У свою чергу, вже при невеликих позитивних значеннях “x” функція різко зростає, при цьому швидкість її збільшення постійно збільшується також за експоненціальним законом, що можна показати, якщо взяти похідну від розглянутої функції ((ax)’ = ln(a)*ax, де ln(a) – натуральний логарифм).
Таким чином, експоненціальна залежність – це різка зміна деякої величини як у бік її збільшення, так і убік зменшення.
Приклад з шахової історії
Хорошою демонстрацією значущості експоненціального збільшення об’єктів є стародавня легенда, пов’язана з винаходом шахів. Згідно з цією легендою, для розваги одного індуського короля, якого звали Белкиб, його близький друг Брахман Сисса за 3000 років до нашої ери створив настільну гру шахи.
Король так радий був новій грі, що пообіцяв дати Сіссе все, що той забажає. Тоді Брахман Сисса запропонував йому дати стільки зерна, скільки поміститься на 64 шахових клітинах, при цьому на 1-у клітку він поклав 1 зерно, на 2-ю – 2 зерна, на 3-ю – 4 зерна і так далі, щоразу подвоюючи число. Белкиб відразу не зрозумів, наскільки багато йому потрібно віддати зерна, тому без роздумів прийняв пропозицію свого друга.
Кількість зерен, яка поміщається на шаховій дошці згідно описаному принципу, складе 264 = 18 446 744 073 709 551 616 – гігантське число!
Зростання населення планети
Ще одним яскравим прикладом процесів, які описуються відповідно експоненційної залежності, є зростання населення планети. Так, в 1500 році населення планети становило близько 500 млн., в 1800 році, тобто через 300 років, воно подвоїлося і стала дорівнювати 1 млрд., минуло менше 50 років, і населення планети переступив позначку 2 млрд, в даний час кількість жителів на планеті Земля складає 7,5 млрд. чоловік.
Описаний на прикладі людства зростання популяції характерний для будь-якого біологічного виду, будь то ссавець або одноклітинні бактерії. Математично це зростання описується наступною формулою: Nt = N0*ek*t, де Nt і N0 – чисельність популяції в моменти часу t і нульовою, відповідно, k – деякий позитивний коефіцієнт. Дана математична модель росту популяцій отримала назву експоненційної залежності в екології.
Експонентний ріст населення планети змусив задуматися ще на початку XIX століття відомого англійського економіста і демографа Томаса Роберта Мальтуса. Вчений свого часу передбачав, що в середині XIX століття на Землі має настати голод, оскільки виробництво продуктів харчування збільшується лінійно, в той час як чисельність людей на планеті збільшується експоненціально. Мальтус вважав, що єдиним способом досягти рівноваги в розглянутій системі, є масова смертність, викликана війнами, епідеміями та іншими катаклізмами.
Як відомо, учений помилився у своїх похмурих прогнозах, принаймні він помилився з вказаною датою.
Вік археологічних решток
Ще одним яскравим прикладом природних процесів, які відбуваються згідно експоненціальним законом, є розпад радіоактивних елементів. Це фізичне явище, яке полягає в перетворенні ядер важких елементів в ядра більш легких, описується наступною математичною формулою: Nt = N0*e-k*t, де Nt і N0 – кількість ядер більш важкого елемента в момент часу t і в початковий момент відповідно. З цієї формули видно, що вона практично аналогічна такій для зростання біологічної популяції, єдина відмінність полягає в знаку “мінус” в показнику експоненти, який говорить про убутку важких ядер.
Зазначену формулу використовують для визначення віку гірських порід та скам’янілих організмів. В останньому випадку працюють з ізотопом вуглецю 14C, оскільки його період напіврозпаду (час, за який початкове число важких ядер зменшиться вдвічі) є відносно невеликим (5700 років).
Інші процеси, підпорядковується експоненціальним законом
Експоненціальна залежність описує процеси в економіці, хімії і медицині. Наприклад, дози медикаментів, що потрапили в організм людини, зменшуються в часі за експоненціальним законом. В економіці інвестиційний прибуток, виходячи з певного початкового капіталу, розраховується також за експоненціальним законом.
