В математиці зворотні функції – це взаємно відповідні вирази, які звертаються один в одного. Щоб розібратися в тому, що це означає, варто розглянути конкретний приклад. Припустимо, маємо y = cos(x). Якщо взяти від косинус аргументу, то можна знайти значення y. Очевидно, для цього необхідно мати ікс. Але що якщо спочатку дано ігрек? Саме тут справа доходить до суті питання. Для розв’язання задачі потрібно використання оберненої функції. У нашому випадку це косинуса.
Після всіх перетворень отримаємо: x = arccos(y).
Тобто, щоб знайти функцію, обернену до даної, досить просто висловити з неї аргумент. Але це працює тільки за умови, якщо отриманий результат буде мати єдине значення (про це далі).
У загальному вигляді можна записати цей факт так: f(x) = y, g(y) = x.
Визначення
Нехай f – функція, областю визначення якої є множина X, а областю значень – множина Y. Тоді, якщо існує g, чиї області виконують протилежні завдання, то f є оборотною.
Крім того, в такому випадку g – єдина, що означає, що існує рівно одна функція, що задовольняє цій властивості (не більше, не менше). Тоді її називають оберненою функцією, і на письмі позначають так: g(x) = f -1(x).
Іншими словами, їх можна розглядати як бінарне відношення. Оборотність має місце бути тільки тоді, коли одному елементу безлічі відповідає одне значення з іншого.
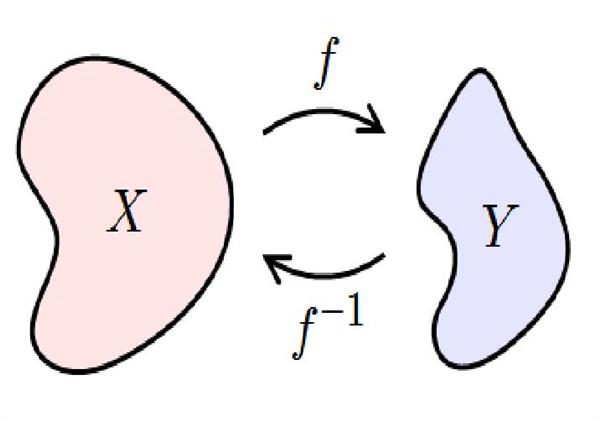
Не завжди існує обернена функція. Для цього кожний елемент y є Y повинен відповідати не більш ніж одному x є X. Тоді f називається взаємно-однозначної або ін’єкцією. Якщо f -1 належить Y, то кожен елемент цієї множини має відповідати деякого x ∈ X. Функції з такою властивістю називаються сюръекциями. Воно виконується за визначенням, якщо Y – зображення f, але це не завжди так. Щоб бути зворотною, функція повинна бути як ін’єкцією, так і сюръекцией. Такі висловлювання називаються биекциями.
Приклад: квадратні і кореневі функції
Функція визначена на [0, ∞) і заданна формулою f (x) = x2.
Тоді вона не є инъективной, оскільки кожному можливому результату Y (крім 0) відповідає два різних X – один додатний і один від’ємний, тому вона не оборотна. В такому випадку буде неможливо отримати вихідні дані з отриманих, що суперечить теорії. Вона буде неинъективной.
Якщо область визначення за умовою обмежена неотрицательными величинами, то все буде працювати як і раніше. Тоді вона биективна і, отже, оборотна. Зворотну функцію тут називають позитивною.
Примітка по запису
Нехай позначення f -1 (x) може заплутати людину, але ні в якому разі не можна використовувати його так: (f (x))- 1. Воно відсилає до зовсім іншого математичного поняття і не має нічого спільного з оберненою функцією.
У відповідності з загальними правилами деякі автори використовують вирази типу sin-1 (x).
Однак інші математики вважають, що це може викликати плутанину. Щоб уникнути подібних труднощів, зворотні тригонометричні функції часто позначається за допомогою префікса “arc” (c латинського дуга). У нашому випадку мова йде про арксинусе. Також зрідка можна зустріти приставку “ar” або “inv” для деяких інших функцій.
