Однією з геометричних фігур, властивості яких вивчають у школах у курсі стереометрії, є піраміда. Розглянемо, що собою являє ця фігура, а також детально охарактеризуємо важливий лінійний параметр – бічне ребро піраміди.
Піраміда як фігура геометрії
Перш ніж розглядати поняття про бічному ребрі піраміди, слід дати визначення цієї просторової фігури. Якщо говорити коротко, то піраміда являє собою поверхню, обмежену однією n-кутником і n трикутниками. Малюнок нижче показує один з можливих варіантів цієї фігури.
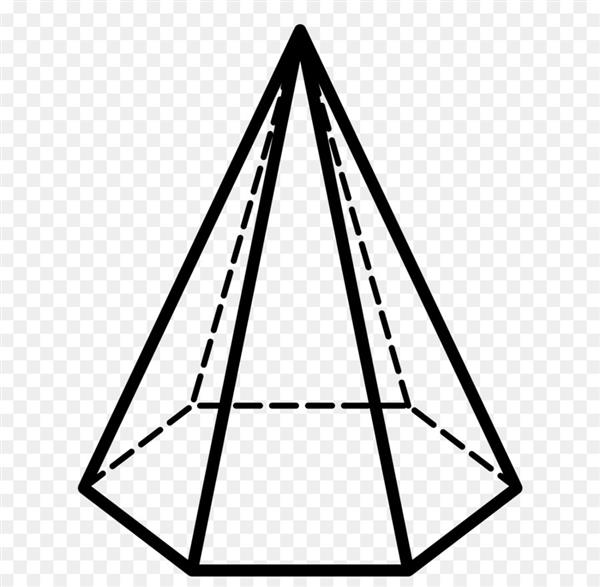
З геометричної точки зору отримати піраміду можна таким способом: взяти n-кутник і з’єднати всі його кути з деякою точкою в просторі, яка не повинна лежати в площині n-кутника.
Зауважимо, що, незалежно від кількості сторін n у вихідному многокутнику, завжди при з’єднанні його кутів з єдиною точкою виходять трикутники. Їх сукупність утворює бічну поверхню піраміди, а вихідний багатокутник є її підставою. Точка, в якій поєднуються всі трикутники, отримала назву вершини піраміди.
Елементи піраміди
Кожна піраміда утворена трьома головними елементами:
- гранями;
- ребрами;
- вершинами.
Граней чи сторін у фігури завжди n + 1. Це легко бачити на наведеному в попередньому пункті малюнку. Шестикутні підстава є однією гранню. Решта 6 сторін являють собою трикутники, що спираються на сторони підстави і перетинаються у вершині піраміди.
Ребра являють собою сукупність точок перетину сусідніх граней. Фігура має два типи цих елементів:
- ребра основи;
- бічні ребра піраміди.
Їх кількості, незалежно від числа сторін n підстави, завжди дорівнюють один одному, тобто фігура має 2 × n ребер. Якщо з ребрами підстави все зрозуміло (вони є сторонами n-кутника), то для бічних ребер слід уточнити, що вони являють собою відрізки, що з’єднують кути підстави з висотою розглянутої фігури.
Нарешті, третім типом елементів піраміди будуть вершини. Біля фігури є n + 1 вершина. Однак n з них утворені підставою і двома бічними гранями. Лише одна єдина вершина не пов’язана з підставою. Вона відіграє важливу роль при вивченні кількісних характеристик піраміди, наприклад, її висоти або апофемы.
Правильні піраміди
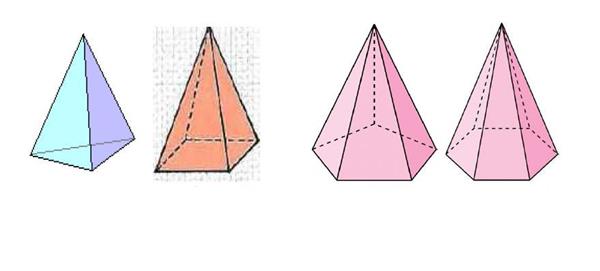
Піраміди можуть бути похилими прямими правильними і неправильними, опуклими й увігнутими. Всі названі типи фігур відрізняються один від одного багатокутним підставою і особливостями поведінки висоти.
Припустимо, що є піраміда, у якої висота (опущений з вершини до основи перпендикуляр) падає на багатокутник точно в його геометричному центрі. У цьому випадку фігура називається прямою. Якщо ж багатокутник є рівностороннім, то крім прямої, піраміда також буде правильною. Нагадаємо, що центр геометричний плоскої фігури аналогічний центру мас у фізиці. Для квадрата він збігається з точкою перетину діагоналей, а для трикутника – з точкою, де медіани перетинаються.
Піраміди правильні зручно вивчати через їх симетрії. Так, бічні ребра правильної піраміди і її бічні грані рівні один одному. Окремим випадком є ситуація, коли бічні грані будуть утворені рівносторонніми трикутниками.
Далі розглянемо, якими формулами слід користуватися, щоб визначити розміри бічних ребер піраміди — правильної чотирикутної і трикутної.
Трикутна піраміда
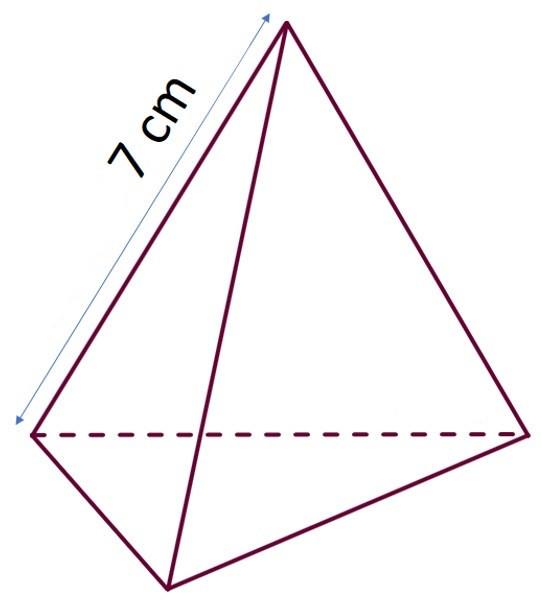
Існують чотири лінійних параметрів, які описують розміри правильної піраміди. До них відносяться сторона підстави a, бічне ребро b, висота h і апофема hb. Нижче наведемо формули, які дозволяють розрахувати довжину бічного ребра для правильної трикутної піраміди. Підстава цієї фігури є трикутник з рівними сторонами, що дозволяє записати такі рівності:
b = √(hb2 + a2/4);
b = √(h2 + a2/3).
Обидві формули є наслідком теореми Піфагора для трикутників, в яких бічне ребро b є гіпотенузою.
Чотирикутна піраміда
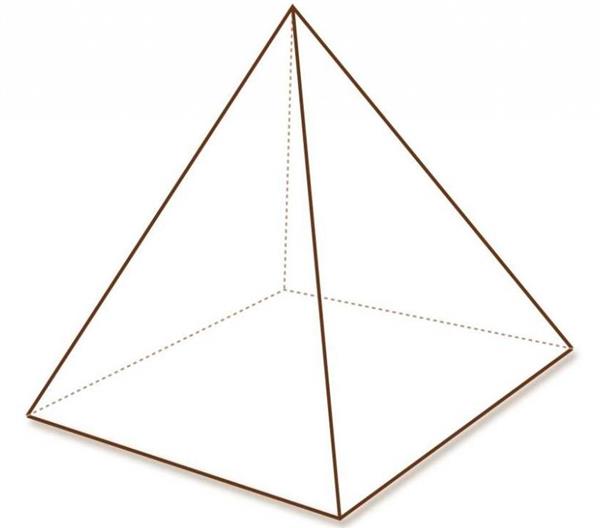
Ця фігура, мабуть, є найвідомішою серед інших пірамід завдяки величним древнім єгипетським споруд. Бічне ребро піраміди правильної чотирикутної можна визначити за такими формулами:
b = √(hb2 + a2/4);
b = √(h2 + a2/2).
Як і в попередньому випадку, ці вирази є наслідком властивості катетів і гіпотенузи прямокутного трикутника.
Зазначимо, що формула розрахунку бічного ребра правильної чотирикутної піраміди через її апофему і сторону підстави аналогічна такій для трикутної фігури. Це збіг не є випадковим, оскільки бічні грані обох пірамід – це рівнобедрені трикутники.
Завдання на визначення бічного ребра піраміди Хеопса

Кожна людина знає, що перше чудо світу – піраміда Хеопса, має запаморочливими розмірами. Вона є найбільшою з усіх пірамід, що знаходяться в єгипетській Гізі. Сторони її основи утворюють квадрат з точністю до декількох десятків сантиметрів. Середня довжина сторони піраміди оцінюється в 230,363 метра. Висота піраміди в даний час складає близько 137 метрів, однак вихідна висота кам’яного гіганта була 146,50 метрів.
Скористаємося наведеними вище цифрами, щоб визначити, чому дорівнює бічне ребро правильної чотирикутної піраміди, присвяченій фараона Хеопсу.
Оскільки нам відома висота h і довжина сторони a монумента, то слід застосувати таку формулу для b:
b = √(h2 + a2/2).
Підставляючи в неї відомі дані, отримуємо, що бічне ребро правильної чотирикутної піраміди дорівнює 273 метра, що трохи менше периметру футбольного поля (300 метрів).

