Ознайомившись з матеріалом, читач зрозуміє, що планіметрія – це зовсім не складно. У статті наведено найважливіша теоретична інформація та необхідні для вирішення конкретних завдань формули. По полицях розкладені важливі затвердження та властивості фігур.
Визначення і важливі факти
Планіметрія – це розділ геометрії, який розглядає об’єкти на плоскій двовимірної поверхні. Можна виділити деякі відповідні приклади: квадрат, коло, ромб.
Серед усього іншого варто виділити точку і пряму. Вони є двома основними поняттями планіметрії.

Вже на них будуються всі решта, наприклад:
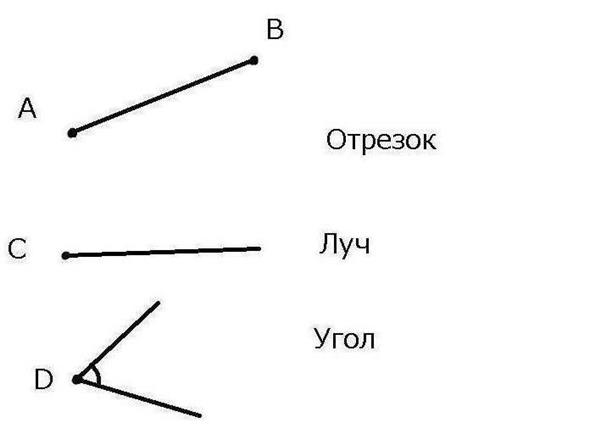
- Відрізок – це частина прямої лінії, обмежена двома точками.
- Промінь – об’єкт, аналогічний відрізку, проте, має кордон лише з одного боку.
- Кут, який складається з двох променів, що виходять з однієї точки.