У шкільному курсі геометрії вивчаються властивості різних видів призм, включаючи шестикутну. Остання часто зустрічається при розгляді кристалічних решіток металів, тому знання її характеристик важливо при визначенні властивостей цього класу матеріалів. Дана стаття присвячена питанню площі основи правильної шестикутної призми.
Об’ємна фігура – призма
В геометрії під призмою розуміють таку фігуру, яка утворена двома рівними багатокутниками, розташованими паралельно один одному, і деяким числом паралелограмів, що з’єднують вершини названих багатокутників. Якщо основа утворено гратки з n вершинами, то кількість паралелограмів також буде дорівнює n.
Призми характеризуються за типом багатокутника в підставі (правильні і неправильні трикутні, чотирикутні і так далі), який може бути увігнутих і опуклих, і по куту між бічними гранями (параллелограммами) і підставою (прямокутні і косокутні).
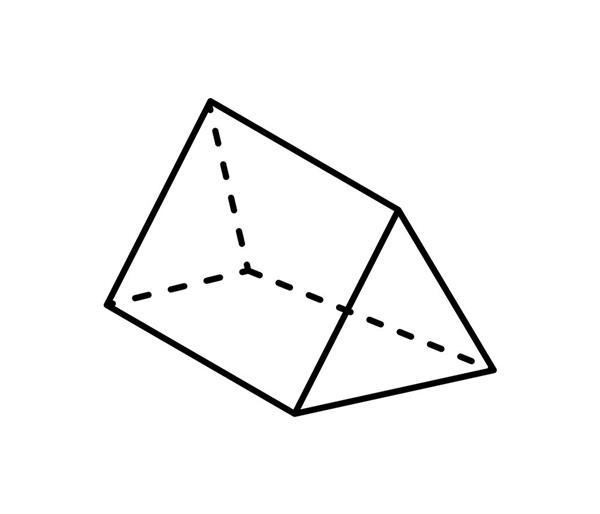
Основними елементами будь-якої призми є її межі (М), ребра (Р) і вершини (В). На малюнку вище наведена для прикладу трикутна призма. Як видно, вона має 6 вершин (3 для кожного підстави). Нижче наведена розгортка цієї призми. Малюнок показує, що вона складається з 5 граней: 2 трикутника і 3 прямокутника.
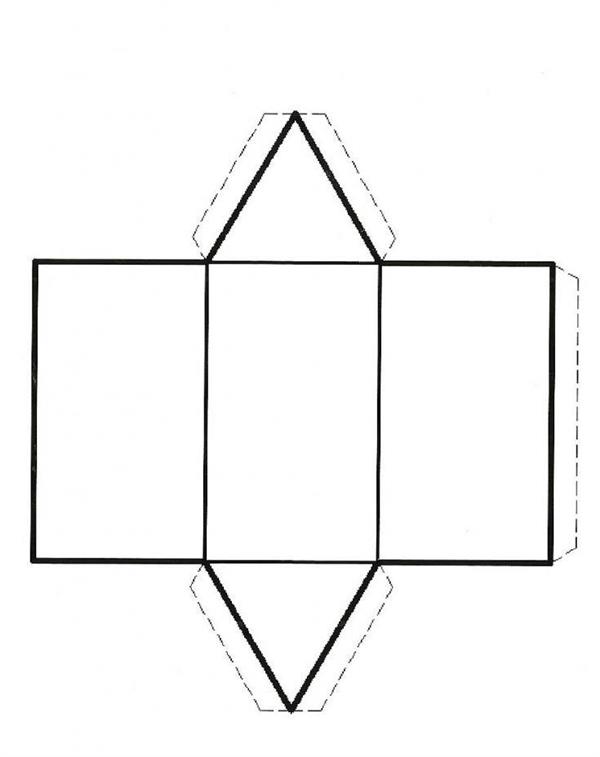
Щоб порахувати число ребер розглянутої фігури, слід застосувати теорему Ейлера:
Р = В + Г – 2
Цей вираз дає число ребер для цієї призми, рівну 9. Дійсно, якщо звернутися до тривимірного зображення призми вище, то можна побачити, що 6 ребер утворюють підстави фігури, і ще 3 ребра є результатом перетину прямокутників.

