Якщо лінійне переміщення тіл описують в класичній механіці за допомогою законів Ньютона, характеристики руху механічних систем по кругових траєкторіях обчислюють за допомогою спеціального вираження, яке називається рівнянням моментів. Про які моменти йде мова і в чому полягає зміст цього рівняння? Ці та інші питання розкриваються в статті.
Момент сили
Всім добре відома ньютоновская сила, яка, діючи на тіло, призводить до повідомлення йому прискорення. Коли ж така сила додається до об’єкта, який закріплений на деякій осі обертання, то цю характеристику називають моментом сили. Рівняння моменту сили може бути записане в такому вигляді:
M = L*F
Малюнок, що пояснює це вираз, наведено нижче.
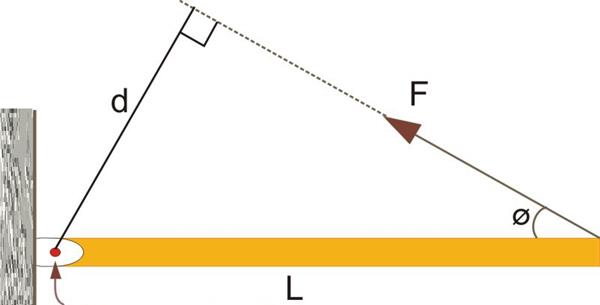
Тут видно, що сила F спрямована до вектора L під кутом Φ. Сам же вектор L покладається спрямованим від осі обертання (вказана стрілкою) до точки додатку F.
Наведена вище формула являє собою добуток двох векторів, тому величина M також є спрямованою. Куди буде повернутий момент сили M? Це можна визначити за правилом правої руки (чотири пальці спрямовані вздовж траєкторії від кінця вектора L до кінця F, а відставлений великий палець показує напрям M).
На малюнку вище вираз для моменту сили в скалярному вигляді прийме форму:
M = L*F*sin(Φ)
Якщо уважно вдивитися в малюнок, то можна побачити, що L*sin(Φ) = d, тоді маємо формулу:
M = d*F
Величина d є важливою характеристикою при обчисленні моменту сили, оскільки вона відображає ефективність F прикладеної до системи. Цю величину прийнято називати важелем сили.
Фізичний сенс M полягає в здатності сили зробити обертання системи. Цю здатність може відчути на собі кожен, якщо буде відкривати двері за ручку, штовхаючи її близько петель, або ж спробує відкрутити гайку коротким і довгим ключем.

