Момент інерції і теорема Штейнера

Відомий швейцарський математик Якоб Штейнер, довів теорему про паралельних осях і моменті інерції, яка тепер носить його прізвище. Ця теорема постулює, що момент інерції для абсолютно будь-якого твердого тіла довільної геометрії щодо деякої осі обертання дорівнює сумі моменту інерції відносно осі, яка перетинає центр мас тіла і паралельна першої, і добутку маси тіла на квадрат відстані між цими осями. Математично ця формулювання записується так:
IZ = IO + m*l2
IZ і IO – моменти інерції щодо осі Z і паралельної їй осі O, яка проходить через центр мас тіла, l – відстань між прямими Z O.
Теорема дозволяє, знаючи величину IO, розрахувати будь-який інший момент IZ відносно осі, яка паралельна O.
Доказ теореми
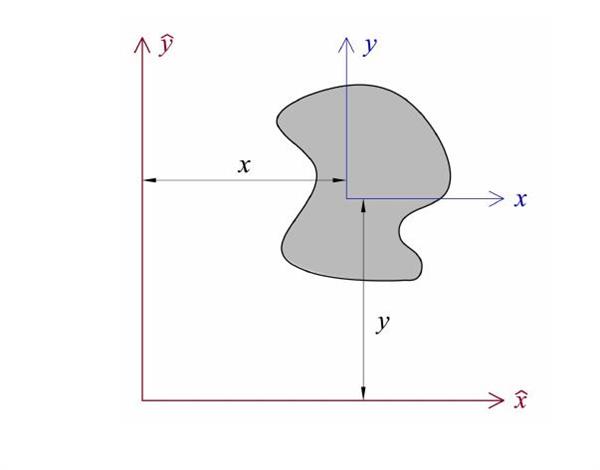
Формулу теореми Штейнера можна легко отримати самостійно. Для цього розглянемо довільне тіло на площині xy. Нехай початок координат проходить через центр мас цього тіла. Розрахуємо момент інерції IO яка проходить через початок координат перпендикулярно площині xy. Оскільки відстань до будь-якої точки тіла виражається формулою r = √ (x2 + y2), тоді одержуємо інтеграл:
IO = ∫m (r2*dm) = ∫m ( (x2+y2) *dm)
Тепер перемістимо паралельно вісь вздовж осі x на відстань l, наприклад, у позитивному напрямку, тоді розрахунок для нової осі моменту інерції буде виглядати наступним чином:
IZ = ∫m (( (x+l)2+y2)*dm)
Розкриємо повний квадрат у дужках і розділимо подынтегральные суми, отримаємо:
IZ = ∫m ( (x2+l2+2*x*l+y2)*dm) = ∫m ( (x2+y2)*dm) + 2*l*∫m (x*dm) + l2*∫mdm
Перше з цих доданків є величиною IO, третій доданок, після проведення інтегрування, дає член l2*m, а ось другий доданок дорівнює нулю. Обнулення вказаного інтегралу пов’язано з тим, що він береться від твору іксів на елементи маси dm, що в середньому дає нуль, так як центр мас знаходиться в початку координат. У результаті, виходить формула теореми Штейнера.
Розглянутий випадок на площині можна узагальнити на об’ємне тіло.