Розрахунок кута трикутника – часто зустрічається завдання курсу шкільної геометрії. Шлях вирішення такої задачі залежить від відомих у ній умов. Ними можуть бути значення інших кутів трикутника, сторін, їх синусів, косинусів. Також варто звертати увагу на вигляд трикутника, описуваного в завданні.
Базове правило
Варто згадати про самому базовому правило для всіх трикутників, з якого прийнято починати, проводячи розрахунок кута трикутника. Воно звучить так: сума градусних мір всіх кутів трикутника дорівнює 180 градусів.
Варіанти рішення
Розрахунок кутів прямокутного трикутника дуже простий. В такому трикутнику один кут завжди дорівнює 90 градусам, відповідно, два інших в сумі дають стільки ж. Якщо в задачі вже відомі значення двох інших кутів, то ви можете швидко знайти третій, віднявши суму відомих кутів з суми кутів всього трикутника.
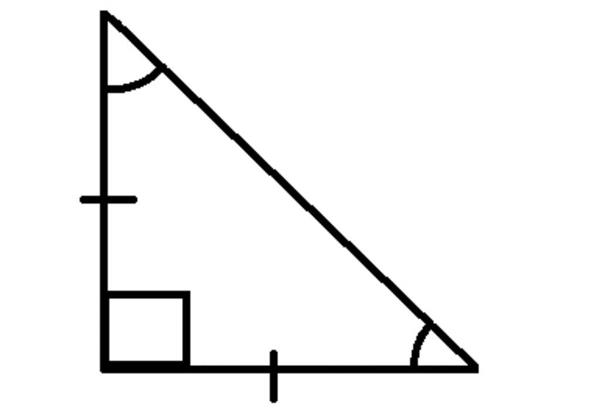
Також можна проводити розрахунок кута трикутника за допомогою теореми синусів, косинусів, тангенсів та котангенсов, знаючи дві будь-які його боку, таким чином:
- тангенс кута дорівнює відношенню противолежащей сторони до прилеглій;
- синус – противолежащей сторони до гіпотенузі;
- косинус – відношенню прилеглій сторони до гіпотенузі.
В завданні вам також можуть знадобитися дані про биссектрисах і медианах трикутника, проведених з невідомого кута.
Слід нагадати, що медіана – це лінія, що з’єднує кут і середину противолежащей сторони. Бісектриса – лінія, делящая кут навпіл. Не варто плутати їх з висотою і навпаки.
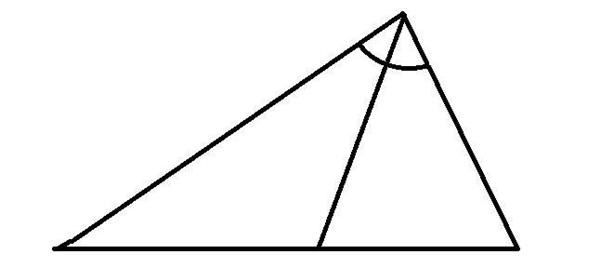
Якщо медіана ділить противолежащую куті сторону навпіл, при цьому отримані кути в невідомому трикутнику рівні, то цей кут дорівнює 90 градусам.
Якщо бісектриса ділить кут навпіл, та до того ж ми знаємо один з кутів трикутника і кут, який належить гіпотенузі і проведеної до неї бісектрисі, то зможемо знайти половину шуканого кута.
Всі ці правила допоможуть вам провести розрахунок кута трикутника.

