Будь-яка фізична величина, яка пропонується в математичних рівняннях при вивченні того чи іншого явища природи, несе певний сенс. Не є винятком з цього правила і момент інерції. Фізичний зміст цієї величини докладно розглянуто в даній статті.
Момент інерції: математичне формулювання
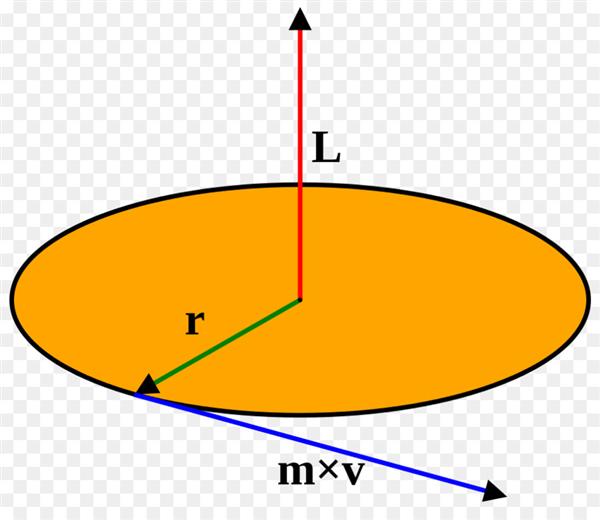
В першу чергу слід сказати, що розглянута фізична величина використовується для опису систем обертання, тобто таких рухів об’єкта, які характеризуються круговими траєкторіями навколо деякої осі або точки.
Наведемо математичну формулу моменту інерції для матеріальної точки:
I = m*r2.
Тут m і r – маса і радіус обертання частинки (відстань до осі) відповідно. Будь-яке тверде тіло, яким би складним воно не було, подумки можна розбити на матеріальні точки. Тоді формула моменту інерції в загальному вигляді буде мати вигляд:
I = ∫mr2dm.
Цей вираз справедливий завжди, причому не тільки для тривимірних, але і для двовимірних (одновимірних) тіл, тобто для площин і стрижнів.
З цих формул важко зрозуміти сенс фізичний моменту інерції, однак можна зробити важливий висновок: він залежить від розподілу маси в тілі, яке обертається, а також від відстані до осі обертання. Причому залежність від r є більш різкою, ніж від m (див. знак квадрата у формулах).