Типовою геометричної завданням є знаходження кута між прямими. На площині, якщо відомі рівняння прямих, їх можна накреслити та виміряти транспортиром кут. Однак цей спосіб трудомісткий і не завжди можливий. Щоб дізнатися названий кут, не обов’язково зображувати прямі, його можна обчислити. Як це робиться, відповість дана стаття.
Пряма і її векторне рівняння
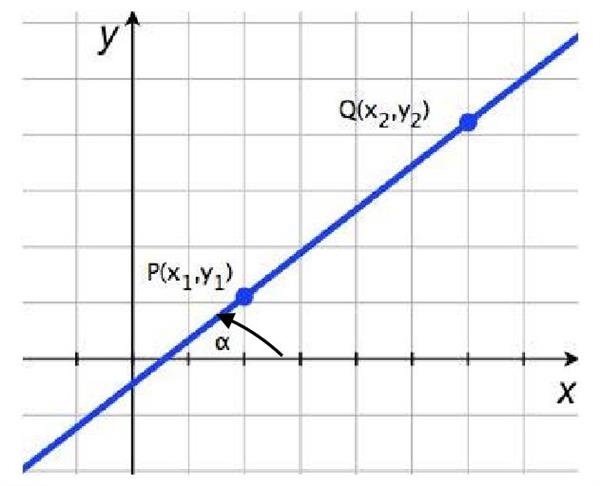
Кожну пряму можна представити у вигляді вектора, який починається в -∞ і закінчується в +∞. При цьому вектор проходить через деяку точку простору. Таким чином, всі вектори, які можна накреслити між двома будь-якими точками прямої, будуть паралельні один одному. Це визначення дозволяє задати рівняння прямої у векторному вигляді:
(x; y; z) = (x0; y0; z0) + α*(a; b; c)
Тут вектор з координатами (a; b; c) є направляючим для цієї прямої, що проходить через точку (x0; y0; z0). Параметр α дозволяє переводити зазначену точку в будь-яку іншу для цієї прямої. Це рівняння інтуїтивно зрозуміло, і з ним легко працювати як в тривимірному просторі, так і на площині. Для площині воно не буде містити координати z і третій компоненти направляючого вектора.
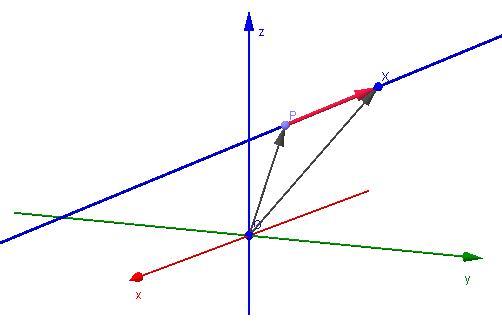
Зручність виконання розрахунків та вивчення взаємного положення прямих завдяки використанню векторного рівняння пов’язано з тим, що відомий її напрямний вектор. Його координати застосовуються для обчислення кута між прямими і відстані між ними.
Загальне рівняння прямої на площині
Запишемо в явному вигляді векторне рівняння прямої для двовимірного випадку. Воно має вигляд:
x = x0 + α*a;
y = y0 + α*b
Тепер розрахуємо для кожного рівності параметр α і приравняем праві частини отриманих рівностей:
α = (x – x0)/a;
α = (y – y0)/b;
(x – x0)/a = (y – y0)/b
Розкриваючи дужки і переносячи всі члени в одну сторону рівності, отримуємо:
1/a*x +(-1/b)*y+y0/b – x0/a = 0 =>
A*x + B*y + C = 0, де A = 1/a, B = -1, b, C = y0/b – x0/a
Отриманий вираз називається загальним рівнянням для прямої, заданої в двовимірному просторі (у тривимірному це рівняння відповідає паралельної осі z площині, а не прямий).
Якщо в цьому виразі явно записати y через x, то вийде наступний вид, відомий кожному школяреві:
y = k*x + p, де k = -A/B, p = -C/B
Це лінійне рівняння однозначно задає на площині пряму. Накреслити її за відомим рівнянням дуже просто, для цього слід по черзі покласти x = 0 і y = 0, зазначити відповідні точки в системі координат і провести пряму, з’єднавши отримані точки.
Формула кута між прямими
На площині дві прямі можуть перетинатися, або бути паралельними один одному. У просторі до цих функцій додається також ще можливість існування скрещивающихся прямих. Який би варіант взаємного положення цих одновимірних геометричних об’єктів не був реалізований, кут між ними завжди можна визначити по наступній формулі:
φ = arccos(|(v1*v2)|/(|v1|*|v2|))
Де v1 і v2 – це вектори напрямні для прямого 1 і 2 відповідно. В чисельнику стоїть модуль скалярного добутку, щоб виключити тупі кути і враховувати тільки гострі.
Вектори v1 і v2 можуть бути задані двома або трьома координатами, формула для кута φ при цьому залишається незмінною.
Паралельність і перпендикулярність прямих
Якщо розрахований за формулою вище кут між прямими 2 дорівнює 0 o, то кажуть, що вони є паралельними. Щоб визначити, чи будуть прямі паралельними чи ні, можна не обчислювати кут φ, досить показати, що один напрямний вектор може бути представлений через аналогічний вектор інший прямий, тобто:
v1 = q*v2
Тут q – деяке дійсне число.
Якщо рівняння прямих задані у вигляді:
y = k1*x + p1,
y = k2*x + p2,
то паралельними вони будуть тільки тоді, коли дорівнюють коефіцієнти при x, тобто:
k1 = k2
Довести цей факт можна, якщо розглянути, як виражається коефіцієнт k через координати направляючого вектора прямої.
Якщо кут перетину між прямими дорівнює 90 o, тоді вони називаються перпендикулярними. Для визначення перпендикулярності прямих також не обов’язково обчислювати кут φ, для цього достатньо розрахувати лише скалярний добуток векторів v1 і v2. Воно має бути одно нулю.
У разі скрещивающихся прямих у просторі формулою для кута φ теж можна користуватися. При цьому слід правильно інтерпретувати отриманий результат. Обчислений φ показує величину кута між напрямними векторами прямих, які не перетинаються і не є паралельними.
Завдання №1. Перпендикулярні прямі
Відомо, що рівняння прямих мають вигляд:
(x; y) = (1; 2) + α*(1; 2);
(x; y) = (-4; 7) + β*(-4; 2)
Необхідно визначити, чи є ці прямі перпендикулярними.
Як було сказано вище, для відповіді на запитання достатньо провести розрахунок скалярного добутку векторів направляючих, яким відповідають координати (1; 2) і (-4; 2). Маємо:
(1; 2)*(-4; 2) = 1*(-4) + 2*2 = 0
Оскільки ми отримали 0, то це означає, що ці прямі перетинаються під прямим кутом, тобто є перпендикулярними.
Завдання №2. Кут перетину прямих
Відомо, що два рівняння для прямих мають наступний вигляд:
y = 2*x – 1;
y = -x + 3
Необхідно знайти кут між прямими.
Оскільки коефіцієнти при x мають різну величину, то ці прямі не паралельні. Щоб знайти кут, який утворюється при їх перетині, переведемо кожне з рівнянь у векторний вигляд.
Для першої прямої отримуємо:
(x; y) = (x; 2*x – 1)
В правій частині рівності ми отримали вектор, координати якого залежать від x. Представимо його у вигляді суми двох векторів, причому координати першого будуть містити змінну x, а координати другого будуть складатися винятково з чисел:
(x; y) = (x; 2*x) + (0; – 1) = x*(1; 2) + (0; – 1)
Оскільки x приймає довільні значення, то його можна замінити на параметр α. Векторне рівняння для першої прямої приймає вигляд:
(x; y) = (0; – 1) + α*(1; 2)
Ті ж самі дії проробляємо з другим рівнянням прямої, отримуємо:
(x; y) = (x-x + 3) = (x-x) + (0; 3) = x*(1; -1) + (0; 3) =>
(x; y) = (0; 3) + β*(1; -1)
Ми переписали у векторному вигляді вихідні рівняння. Тепер можна скористатися формулою для кута перетину, підставляючи в неї координати направляючих векторів прямих:
(1; 2)*(1; -1) = -1;
|(1; 2)| = √5;
|(1; -1)| = √2;
φ = arccos(|-1|/(√5*√2)) = 71,565 o
Таким чином, розглянуті прямі перетинаються під кутом 71,565 o, або 1,249 радіан.
Цю задачу можна вирішити інакше. Для цього слід взяти дві довільні точки кожної прямої, скласти з них вектора направляючі, а потім скористатися формулою для φ.
