Кожен чув про таких об’ємних постатей, як куля, циліндр, піраміда і призма. Остання з них є досконалим полиэдром, властивості якого розглядаються у шкільному курсі геометрії в старших класах. У даній статті розкриємо питання, як знайти об’єм прямої призми, в основі якої лежить довільний багатокутник.
Поняття про прямій призмі
Перед визначенням обсягу будь-просторової фігури важливо чітко розібратися, з чим доведеться мати справу. У нашому випадку ми розглянемо пряму, або прямокутну призму. Вона являє собою фігуру, що складається з двох підстав і кількох бічних граней, які перпендикулярні цих підстав. Обидва підстави представлені одним і тим же гратки і є паралельними один одному. Якщо кількість сторін багатокутника прагне до нескінченності, то така пряма призма переходить в циліндр.
Питання перпендикулярності бічних граней і підстав фігури має принципове значення. Як буде показано нижче, саме від цієї властивості залежить кінцева формула для обчислення об’єму прямої, або прямокутної призми. Прямокутної вона називається тому, що її бічні грані є прямокутниками.
Протилежністю прямокутної призми є косоугольная. Як можна здогадатися, відмінність між ними полягає тільки в куті між бічними гранями і підставами. У косокутних, або похилої призми цей кут відрізняється від 90o.
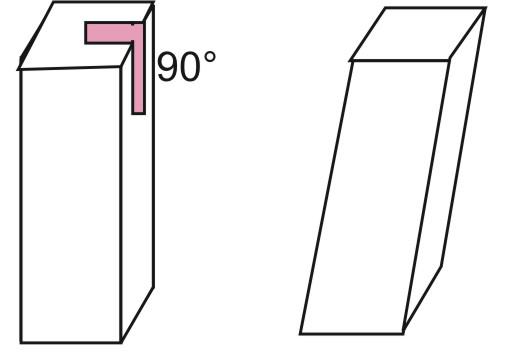
На малюнку вище зображено дві чотирикутні призми, одна з яких є прямий (ліва), а друга – косокутної.

