Окружність – основна фігура в геометрії, властивості якої розглядають в школі у 8 класі. Одна з типових завдань, пов’язаних з окружністю, полягає в знаходженні площі деякої її частини, яка носить назву кругового сектора. У статті наводяться формули площі сектора і його довжини дуги, а також приклад їх використання для вирішення конкретної задачі.
Поняття про колі та колі
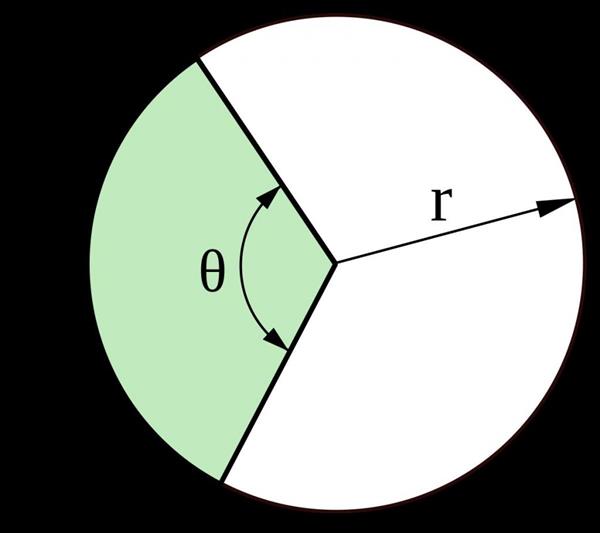
Перед тим як приводити формулу площі сектора кола, розглянемо, що собою являє зазначена фігура. Згідно математичного визначенням, під колом розуміють таку фігуру на площині, всі точки якої рівновіддалені від деякої однієї точки (центру).
Коли розглядають коло, то користуються такою термінологією:
- Радіус – відрізок, який проводиться від центральної точки до кривої колу. Його прийнято позначати буквою R.
- Діаметр – це відрізок, який з’єднує дві точки кола, але при цьому проходить також через центр фігури. Його зазвичай позначають буквою D.
- Дуга – це частина кривої колу. Вимірюють її або в одиницях довжини, або з використанням кутів.
Коло – ще одна важлива фігура геометрії, він являє собою сукупність точок, яка обмежена кривою колу.