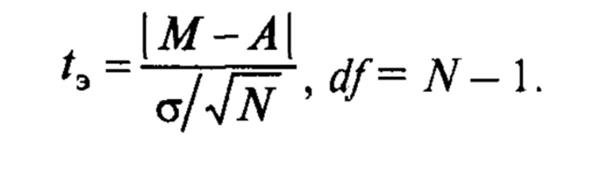Загальний питання при порівнянні двох наборів вимірювань полягає в тому, чи слід використовувати процедуру параметричного тестування або непараметрическую. Найчастіше, використовуючи симуляцію, порівнюють декілька параметричних і непараметричних тестів, таких як t-тест, нормальний тест (параметричні критерії), рівня Уілкоксона, оцінки Ван-дер-Вальдена і т. д.(непараметричні).
Параметричні тести припускають базові статистичні розподілу даних. Тому необхідно виконати кілька умов дійсності, щоб їх результат був надійним. Непараметричні тести не залежать від будь-якого розподілу. Таким чином, вони можуть застосовуватися, навіть якщо параметричні умови дійсності не виконуються. У даній статті ми розглянемо параметричний метод, а саме – коефіцієнт кореляції Стьюдента.
Параметричний метод порівняння вибірок (t-Ст’юдента)
Методи класифікуються на основі того, що ми знаємо про суб’єктів, яких ми аналізуємо. Основна ідея полягає в тому, що існує набір фіксованих параметрів, які визначають імовірнісну модель. Всі види коефіцієнта Стьюдента – це параметричні методи.
Ними часто є ті методи, при аналізі яких ми бачимо, що суб’єкт є приблизно нормальним, тому перед тим, як використовувати критерій, слід здійснити перевірку на нормальність. Тобто розміщення ознак в таблиці розподілу Стьюдента (в обох вибірках) не повинне істотно відрізнятися від нормального і зобов’язана відповідати або приблизно узгоджуватися з указаним параметром. Для нормального розподілу існує два показники: середнє і стандартне відхилення.
Застосування t-критерію стьюдента проводиться при перевірці гіпотез. Він дозволяє перевірити припущення, застосовне до випробуваним. Найчастіше цей критерій застосовується для того, щоб перевірити, чи рівні середні значення двох вибірках, але також може застосовуватися і для одного.
Слід додати, що перевага використання параметричного тесту замість непараметричного полягає в тому, що перше буде мати більшу статистичну потужність, ніж останнім. Іншими словами, параметричний тест здатний привести до відмови від нульової гіпотези.