Площа шестикутника
Отримаємо формулу площі правильного шестикутника. Для цього розглянемо цю плоску фігуру, яка зображена на малюнку нижче.
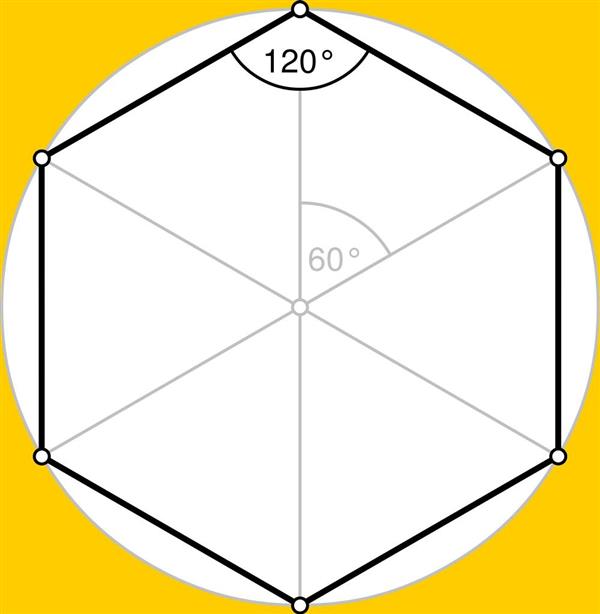
Видно, що багатокутник складається з шести однакових сторін, які утворюють кут 120 o. Оскільки цих кутів шість, то їх сума складе 720o.
Рисунок також показує, що правильний шестикутник гармонійно вписується в коло. Якщо з’єднати центр кола з кожною вершиною фігури, то отримаємо 6 однакових трикутників. Оскільки кутова міра всій окружності становить 360o, то відповідні кути трикутника дорівнюють 60o (360o/6). Вони позначені на малюнку. Оскільки кожен сірий відрізок ділить кут шестикутника навпіл, то два трикутника також рівні за 60o. Це означає, що зображені 6 трикутників є рівносторонніми. Довжина кожної з їх сторін дорівнює стороні шестикутника, позначимо її буквою a.
З курсу геометрії відомо, що площа S3 будь-якого трикутника дорівнює добутку його висоти h на бік a, до якої вона проведена, поділеному навпіл, тобто:
S3 = h*a/2
Довжину h легко обчислити, використовуючи поняття про тригонометричної функції. Вона дорівнює:
h = a*cos(30o) = a*√3/2
Тоді площа всього трикутника дорівнює:
S3 = √3*a2/4
Множачи цю площу на 6, отримуємо формулу площі правильного шестикутника:
S6 = 6*S3 = 3*√3*a2/2
Для повноти інформації слід зазначити, що існує формула площі правильного багатокутника з довільною кількістю сторін n. Нижче наведено відповідний вираз:
Sn = n/4*a2*ctg(pi/n)
Якщо підставити в це вираження значення n = 6, то ми отримаємо формулу площі основи правильної шестикутної призми, яка збігається з наведеною вище.
Зауважимо, що поділ шестикутника на 6 рівносторонніх трикутників означає, що шестикутна призма складається з 6 правильних трикутних призм.