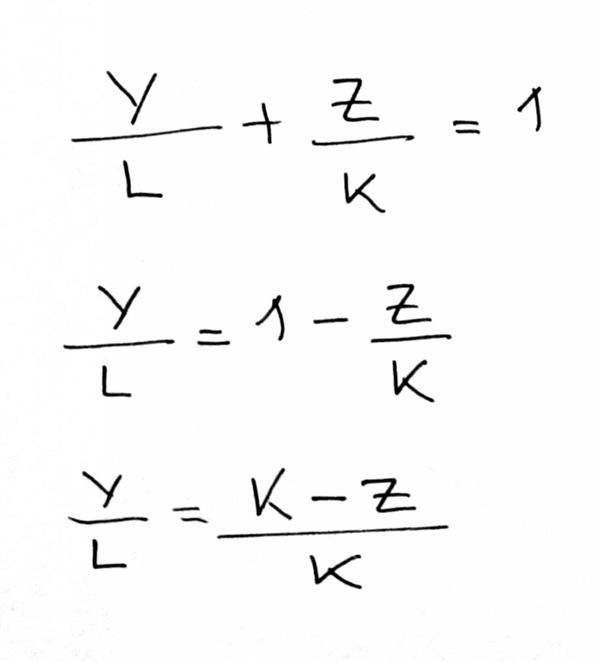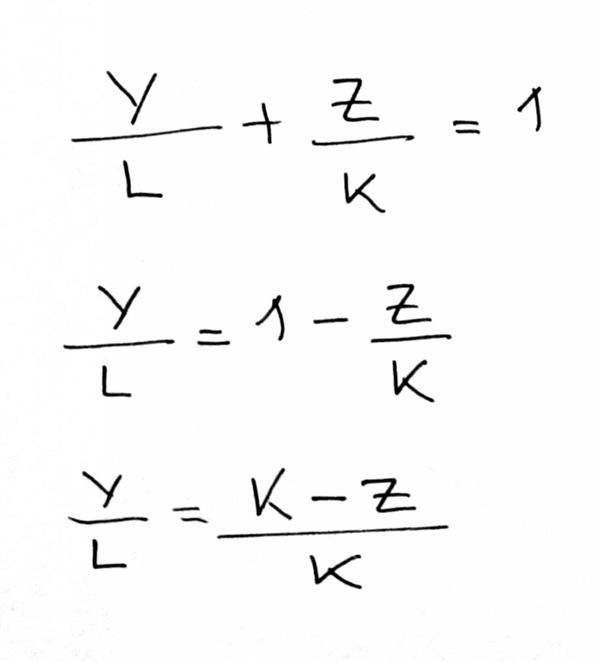Для визначення паралельності та перпендикулярності площин, а також для розрахунку відстаней між цими геометричними об’єктами, зручно користуватися тим чи іншим видом числових функцій. Для яких завдань зручно використовувати рівняння площини у відрізках? У цій статті розглянемо, що це і як використовувати в практичних завданнях.
Що являє собою рівняння у відрізках?
Площину можна задати в тривимірному просторі кількома способами. У цій статті деякі з них будуть наведені під час розв’язування задач різного типу. Тут же дамо детальну характеристику рівняння площини у відрізках. Воно в загальному випадку має наступний вигляд:
x/p + y/q + z/r = 1.
Де символами p, q, r позначені деякі конкретні числа. Це рівняння можна легко перевести у вираз загального виду та інші форми числових функцій для площини.
Зручність запису рівняння у відрізках полягає в тому, що воно містить явні координати перетину площини з перпендикулярними осями координат. На осі x відносно початку координат площину відсікає відрізок завдовжки p, y дорівнює q, z – довжиною r.
Якщо який-небудь з трьох змінних не міститься в рівнянні, то це означає, що через відповідну вісь площину не проходить (математики кажуть, що перетинає в нескінченності).
Далі наведемо кілька завдань, в яких покажемо, як працювати з цим рівнянням.