Динаміка та кінематика – це два важливих розділу фізики, які вивчають закони переміщення об’єктів у просторі. Перший розглядає діючі на тіло сили, другий же займається безпосередньо характеристиками динамічного процесу, не вникаючи в причини того, що його викликало. Знання цих розділів фізики необхідно застосовувати для успішного рішення завдань на рух по похилій площині. Розглянемо це питання в статті.
Основна формула динаміки
Звичайно ж, мова йде про другому законі, який постулював Ісаак Ньютон в XVII столітті, вивчаючи механічний рух твердих тел. Запишемо його в математичній формі:
F = m*a
Дію зовнішньої сили F викликає появу лінійного прискорення a у тіла масою m. Обидві векторні величини (F і a) спрямовані в одну і ту ж сторону. Сила у формулі є результатом дії на тіло усіх сил, які присутні в системі.
У разі руху обертання другий закон Ньютона записується у вигляді:
M = I*α
Тут M та I – моменти сил інерції і, відповідно, α – кутове прискорення.
Формули кінематики
Рішення завдань на рух по похилій площині вимагає знання не тільки головної формули динаміки, але і відповідних виразів кінематики. Вони пов’язують рівності прискорення, швидкість і пройдений шлях. Для равноускоренного (равнозамедленного) прямолінійного руху застосовуються наступні формули:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Тут v0 – значення початкової швидкості тіла, S – пройдений за час t шлях вздовж прямолінійної траєкторії. Знак “+” слід поставити, якщо швидкість тіла збільшується з плином часу. В іншому випадку (равнозамедленное рух) слід використовувати у формулах знак “-“. Це важливий момент.
Якщо рух здійснюється по круговій траєкторії (обертання навколо осі), тоді слід використовувати такі формули:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Тут α і ω – кутові прискорення і швидкість, відповідно, θ – кут повороту обертового тіла за час t.
Лінійні і кутові характеристики друг з одним пов’язані формулами:
a = α*r;
v = ω*r
Тут r – радіус обертання.
Рух по похилій площині: сили
Під цим рухом розуміють переміщення деякого об’єкта вздовж плоскої поверхні, яка нахилена під певним кутом до горизонту. Прикладами може служити зісковзування бруска по дошці або кочення циліндра по металевому нахиленому листу.
Для визначення характеристик розглянутого типу руху необхідно в першу чергу знайти всі сили, які діють на тіло (брусок, циліндр). Вони можуть бути різними. У загальному випадку це можуть бути наступні сили:
- тяжкості;
- реакції опори;
- тертя кочення та/або ковзання;
- натяг нитки;
- сила зовнішньої тяги.
Перші три з них присутні завжди. Існування останніх двох залежить від конкретної системи фізичних тел.
Щоб вирішувати завдання на переміщення по похилій площині необхідно знати не тільки модулі сил, але і їх напрямки дії. У випадку, якщо тіло по площині скочується, сила тертя невідома. Однак вона визначається з відповідної системи рівнянь руху.

Методика рішення
Рішення задач даного типу починається з визначення сил та їх напрямів дії. Для цього в першу чергу розглядають силу тяжіння. Її варто розкласти на два складових вектора. Один з них повинен бути спрямований уздовж поверхні похилої площини, а другий повинен бути перпендикулярний їй. Перша складова сили тяжіння, у випадку руху тіла вниз, забезпечує його лінійне прискорення. Це відбувається в будь-якому випадку. Друга дорівнює силі реакції опори. Всі ці показники можуть мати різні параметри.
Сила тертя при русі по похилій площині завжди спрямована проти переміщення тіла. Якщо мова йде про ковзанні, то обчислення досить прості. Для цього слід використовувати формулу:
Ff = µ*N
Де N – реакція опори, µ – коефіцієнт тертя, який не має розмірності.
Якщо в системі присутні тільки зазначені три сили, тоді їх результуюча вздовж похилої площини буде дорівнює:
F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a
Тут φ – це кут нахилу площини до горизонту.
Знаючи силу F, можна за законом Ньютона визначити лінійне прискорення a. Останнє, в свою чергу, використовується для визначення швидкості руху по похилій площині через відомий проміжок часу, пройденого тілом відстані. Якщо вникнути, то можна зрозуміти, що все не так вже й складно.
У випадку, коли тіло скочується по похилій площині без прослизання, сумарна сила F буде дорівнювати:
F = m*g*sin(φ) – Fr = m*a
Де Fr – сила тертя кочення. Вона невідома. Коли тіло котиться, то сила тяжіння не створює моменту, оскільки прикладена до осі обертання. У свою чергу, Fr створює наступний момент:
M = Fr*r = I*α
Враховуючи, що ми маємо два рівняння і дві невідомих (α a пов’язані один з одним), можна легко вирішити цю систему, а значить, і завдання.
Тепер розглянемо, як використовувати описану методику при вирішенні конкретних завдань.
Завдання на рух бруска по похилій площині
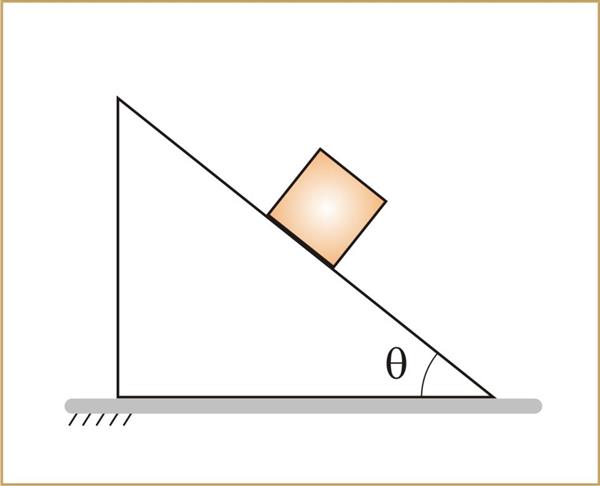
Дерев’яний брусок знаходиться у верхній частині похилій площині. Відомо, що вона має довжину 1 метр і розташовується під кутом 45o. Необхідно обчислити, за який час брусок опуститься цій площині в результаті ковзання. Коефіцієнт тертя прийняти рівним 0,4.
Записуємо закон Ньютона для даної фізичної системи і обчислюємо значення лінійного прискорення:
m*g*(sin(φ) – µ*cos(φ)) = m*a =>
a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с2
Оскільки нам відомо відстань, яку має пройти брусок, то можна записати наступну формулу для шляху при рівноприскореному русі без початкової швидкості:
S = a*t2/2
Звідки слід висловити час, і підставити відомі значення:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 з
Таким чином, час руху по похилій площині бруска складе менше секунди. Зауважимо, що отриманий результат від маси тіла не залежить.
Завдання з скатывающимся по площині циліндром
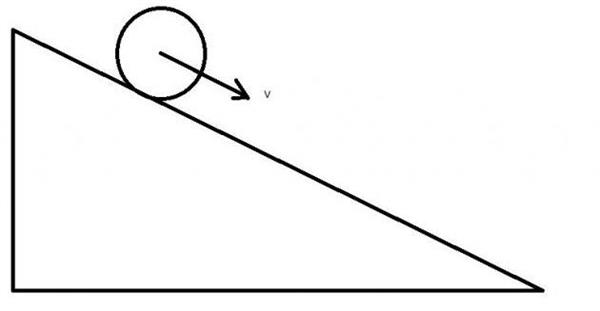
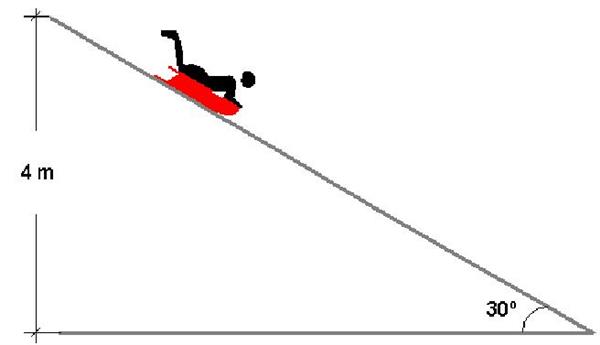
Циліндр радіусом 20 см і масою 1 кг поміщений на похилу під кутом 30 o площину. Слід обчислити його максимальну лінійну швидкість, яку він набере при скачуванні з площини, якщо її довжина становить 1,5 метра.
Запишемо відповідні рівняння:
m*g*sin(φ) – Fr = m*a;
Fr*r = I*α = I*a/r
Момент інерції I циліндра обчислюється за формулою:
I = 1/2*m*r2
Підставимо це значення у другу формулу, виразимо з неї силу тертя Fr і замінимо отриманим виразом її в першому рівнянні, маємо:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) – 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Ми отримали, що лінійне прискорення не залежить від радіуса і маси скочується з площини тіла.
Знаючи, що довжина площині складає 1,5 метра, знайдемо час руху тіла:
S = a*t2/2 =>
t = √(2*S/a)
Тоді максимальна швидкість руху по похилій площині циліндра дорівнює:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Підставляємо всі відомі з умови задачі величини в кінцеву формулу, отримуємо відповідь: v ≈ 3,132 м/c.

