Для успішного рішення завдань з геометрії необхідно чітко розуміти терміни, які використовує ця наука. Наприклад, такими є “пряма”, “площина”, “багатогранник”, “піраміда” та багато інших. У даній статті відповімо на питання, що таке апофема.
Подвійне використання терміна “апофема”
В геометрії значення слова “апофема” або “апотема”, як її ще називають, залежить від того, до якого об’єкта її застосовують. Існує два принципово різних класу фігур, в яких вона є однією з їх характеристик.
В першу чергу це плоскі многокутники. Що таке апофема для багатокутника? Це висота, проведена з геометричного центру фігури до будь-якої з його сторін.
Щоб було зрозуміліше, про що йде мова, розглянемо конкретний приклад. Припустимо, що є правильний шестикутник, показаний нижче на малюнку.
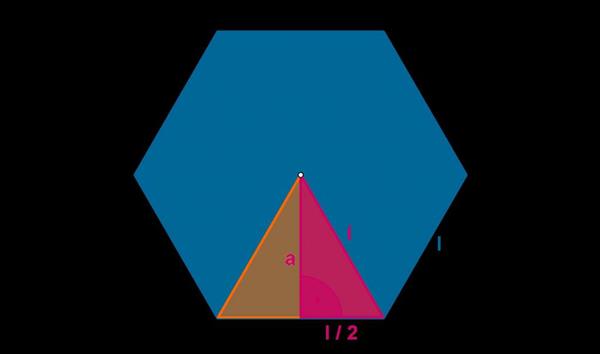
Символом l позначена довжина його сторони, буквою a – апофема. Для зазначеного трикутника вона є не тільки висотою, але і бісектрисою, і медіаною. Нескладно показати, що через сторону l її можна обчислити так:
a = √3/2*l
Аналогічним чином апофема визначається для будь-якого n-кутника.
У другу чергу – це піраміди. Що таке апофема для такої фігури? Це питання потребує більш детального розгляду.
Піраміди і їх апофемы
Для початку дамо визначення піраміді з точки зору геометрії. Ця фігура являє собою об’ємне тіло, утворене однією n-косинцем (заснування) та n трикутниками (бокові сторони). Останні з’єднані в одній точці, яка називається вершиною. Відстань від неї до підстави – це висота фігури. Якщо вона потрапляє на геометричний центр n-кутника, то піраміда називається прямою. Якщо до того ж n-кутник має рівні кути і сторони, то фігура називається правильною. Нижче показаний приклад піраміди.
Що таке апофема для такої фігури? Це перпендикуляр, який з’єднує боку n-кутника з вершиною фігури. Очевидно, що вона являє собою висоту трикутника, що є бічною стороною піраміди.
Апофему зручно використовувати при рішенні геометричних задач з правильними пірамідами. Справа в тому, що для них всі бічні грані є рівними один одному равнобедренными трикутниками. Останній факт означає, що всі n апофем рівні, тому для правильної піраміди можна говорити про однією-єдиною такою прямою.
Апофема правильної чотирикутної піраміди
Мабуть, найбільш наочним прикладом цієї фігури буде знамените перше чудо світу – піраміда Хеопса. Вона знаходиться в Єгипті.
Для такої фігури з правильним n-вугільним підставою можна навести формули, які дозволяють визначити її апофему через довжину a сторони багатокутника, через бічне ребро b і висоту h. Тут запишемо відповідні формули для прямої піраміди з квадратною основою. Апофема hb для неї буде дорівнює:
hb = √(b2 – a2/4);
hb = √(h2 + a2/4)
Перше з цих виразів справедливо для будь-якої правильної піраміди, друге – тільки для чотирикутної.
Покажемо, як ці формули можна використовувати для вирішення задачі.
Геометрична задача
Нехай задана пряма піраміда, що має квадратну основу. Необхідно розрахувати її заснування площа. Апофема піраміди дорівнює 16 см, а її висота в 2 рази більше боку підстави.
Кожен школяр знає: щоб знайти площу квадрата, яким є підстава даної піраміди, слід знати його бік a. Для її знаходження скористаємося наступною формулою для апофемы:
hb = √(h2 + a2/4)
Значення апофемы відомо з умови задачі. Оскільки висота h в два рази більше довжини сторони a, цей вираз можна перетворити наступним чином:
hb = √((2*a)2 + a2/4) = a/2*√17 =>
a = 2*hb/√17
Площа квадрата дорівнює добутку його сторін. Підставляючи отриманий вираз для a, маємо:
S = a2 = 4/17*hb2
Залишається підставити у формулу значення апофемы з умови задачі і записати відповідь: S ≈ 60,2 см2.
