Судячи по популярності запиту “теорема Ферма короткий доказ”, ця математична проблема дійсно багатьох цікавить. Ця теорема була вперше висловлена П’єр де Ферма в 1637 році на краю копії “Арифметики”, де він стверджував, що у нього було її рішення, воно було занадто велике для того, щоб поміститися на краю.
Перше успішне доказ було опубліковано в 1995 році – це було повне доведення теореми Ферма, здійснене Ендрю Уайлсом. Воно було описано як «приголомшливий прогрес», і призвело Уайлса до отримання премії Абеля в 2016 році. Будучи описаним щодо коротко, доказ теореми Ферма також довело більшу частину теореми модульності і відкрило нові підходи до численних інших проблем і ефективним методам підйому модульності. Ці звершення просунули математику на 100 років вперед. Доказ малої теореми Ферма сьогодні не є чимось незвичайним.

Невирішена проблема стимулювала розвиток алгебраїчної теорії чисел в XIX столітті і пошук доведення теореми модульності в XX столітті. Це одна з найпомітніших теорем в історії математики і до повного докази великої теореми Ферма методом ділення вона була в Книзі рекордів Гіннеса як «найбільш складна математична задача», однією з особливостей якої є те, що вона має найбільшу кількість невдалих доказів.
Історична довідка
Піфагорійське рівняння x2 + y2 = z2 має нескінченне число позитивних цілих рішень для x, y і z. Ці рішення відомі як трійці Піфагора. Приблизно в 1637 році Ферма написав на краю книги, що більш загальне рівняння an + bn = cn не має розв’язків у натуральних числах, якщо n є цілим числом, більшим ніж 2. Хоча сам Ферма стверджував, що має рішення свого завдання, він не залишив ніяких подробиць про її доведення. Елементарне доказ теореми Ферма, заявлене її творцем, швидше було його хвастливой вигадкою. Книга великого французького математика була виявлена через 30 років після його смерті. Це рівняння отримало назву «Остання теорема Ферма», протягом трьох з половиною століть залишалося невирішеним математики.
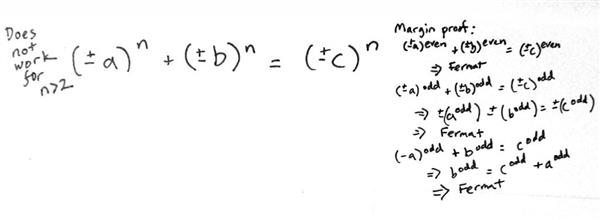
Теорема в кінцевому підсумку стала однією з найбільш помітних невирішених проблем математики. Спроби довести це викликали істотне розвиток теорії чисел, і з плином часу остання теорема Ферма отримала популярність як невирішена проблема математики.
Коротка історія доказів
Якщо n = 4, що доведено самим Ферма, досить довести теорему для індексів n, які є простими числами. Протягом наступних двох століть (1637-1839) гіпотеза була доведена тільки для простих чисел 3, 5 і 7, хоча Софі Жермен оновлювала і доводила підхід, який мав відношення до всього класу простих чисел. В середині 19 століття Ернст Куммер розширив це і довів теорему для всіх правильних простих чисел, в результаті чого нерегулярні прості числа аналізувалися індивідуально. Грунтуючись на роботі Куммера і, використовуючи складні комп’ютерні дослідження, інші математики змогли розширити рішення теореми, маючи на меті охопити всі основні показники до чотирьох мільйонів, але док-в для всіх експонентів раніше було недоступним (це означає, що математики зазвичай вважали рішення теореми неможливим, надзвичайно складним, або недосяжним з сучасними знаннями).
Робота Шимуры і Таниямы
У 1955 році японські математики Горо Шімури і Ютака Таніяма підозрювали, що існує зв’язок між еліптичними кривими і модульними формами, двома абсолютно різними областями математики. Відома в той час, як гіпотеза Таніяма-Шімури-Вейля і (в остаточному підсумку) як теорема модульності, вона існувала сама по собі, без видимого зв’язку з останньої теореми Ферма. Вона сама по собі широко розглядалася як важлива математична теорема, але при цьому вважалася (як і теорема Ферма) неможливою для доказу. У той же час доказ великої теореми Ферма (методом ділення і застосування складних математичних формул) було здійснено лише через півстоліття.
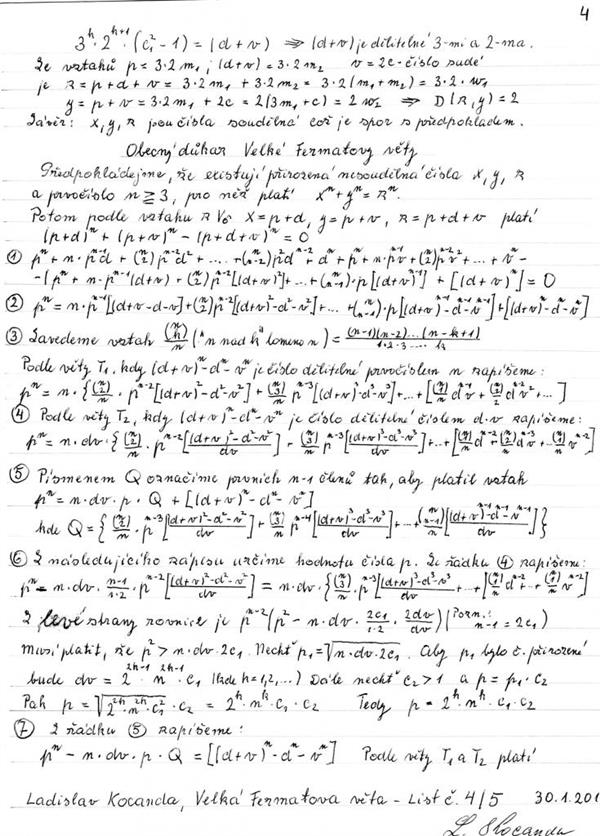
У 1984 році Герхард Фрей помітив очевидну зв’язок між цими двома раніше не пов’язаними і невирішеними проблемами. Повне підтвердження того, що дві теореми були тісно пов’язані, було опубліковано в 1986 році Кеном Рибетом, який ґрунтувався на частковому доказі Жана-П’єра Серра, який довів всі, крім однієї частини, відомої як «гіпотеза епсилона». Простіше кажучи, ці роботи Фрея, Серра і Рібе показали, що якщо б теорема про модульності могла бути доведена, принаймні, для полустабильного класу еліптичних кривих, то й доказ великої теореми Ферма також рано чи пізно буде відкрито. Будь-яке рішення, яке може суперечити останньої теореми Ферма, може також використовуватися, щоб суперечити теоремі модульності. Тому, якщо теорема про модульності виявилася справжньою, то по визначенню не може існувати рішення, що суперечить останньої теореми Ферма, а значить вона незабаром повинна була бути доведена.
Хоча обидві теореми були складними проблемами для математики, які вважаються нерешаемыми, робота двох японців стала першим припущенням про те, як остання теорема Ферма могла б бути продовжена і доведено для всіх чисел, а не лише для деяких. Важливим для дослідників, які обрали тему дослідження, був той факт, що на відміну від останньої теореми Ферма, теорема модульності була основною активною областю досліджень, для якої було розроблено доказ, а не тільки історичну аномалію, тому час, витрачений на її роботу, могло бути виправдано з професійної точки зору. Однак загальна думка полягала в тому, що рішення гіпотези Таниямы-Шимуры виявилося недоцільним.
Велика теорема Ферма: доказ Уайлса
Дізнавшись, що Рибет довів правильність теорії Фрея, англійський математик Ендрю Уайлс, з дитинства цікавиться останньої теореми Ферма і має досвід роботи з еліптичними кривими і суміжними областями, вирішив спробувати довести гіпотезу Таниямы-Шимуры, як спосіб довести останню теорему Ферма. У 1993 році, через шість років після оголошення про своєї мети, таємно працюючи над проблемою рішення теореми, Уайльсу вдалося довести суміжну гіпотезу, що, в свою чергу, допомогло б йому довести останню теорему Ферма. Документ Уайлса був величезним за розміром і масштабом.
Недолік був виявлений в одній частині його оригінальної статті під час рецензування і зажадав ще один рік співпраці з Річардом Тейлором, щоб спільно вирішити теорему. У результаті остаточне доказ Уайлсом великої теореми Ферма не змусило себе довго чекати. В 1995 році воно було опубліковано в значно меншому масштабі, ніж попередня математична робота Уайлса, наочно показуючи, що він не помилився у своїх попередніх висновках про можливості доведення теореми. Досягнення Уайлса була широко розтиражована в популярній пресі і популяризовано в книгах і телевізійних програмах. Інші частини гіпотези Таніяма-Шімури-Вейля, які тепер були доведені і відомі як теорема про модульності, згодом були доведені іншими математиками, які ґрунтувалися на роботі Уайлса в період між 1996 і 2001 роками. За своє досягнення Уайлс був удостоєний честі і отримав численні нагороди, в тому числі, премію Абеля 2016 року.

Доказ Уайлсом останньої теореми Ферма є приватним випадком рішення теореми модульності для еліптичних кривих. Тим не менш, це самий відомий випадок такої масштабної математичної операції. Разом з рішенням теореми Рібе, британський математик також отримав доказ великої теореми Ферма. Остання теорема Ферма і теорема про модульності майже повсюдно вважалися недоказовими сучасними математиками, але Ендрю Уайлс зміг довести всьому науковому світові, що навіть вчені мужі здатні помилятися.
Уайлс вперше оголосив про своє відкриття в середу 23 червня 1993 року на лекції в Кембриджі під назвою «Модульні форми, еліптичні криві і подання Галуа». Однак у вересні 1993 року було встановлено, що його розрахунки містять помилку. Рік потому, 19 вересня 1994 року, в тому, що він назвав «найважливішим моментом його трудового життя», Уайлс натрапив на одкровення, яке дозволило йому виправити рішення задачі до того рівня, коли воно зможе задовольнити математичне співтовариство.

Характеристика роботи
Доказ теореми Ферма Ендрю Уайлсом використовує багато методів з алгебраїчної геометрії і теорії чисел і має багато розгалужень в цих областях математики. Він також використовує стандартні конструкції сучасної алгебраїчної геометрії, такі як категорія схем і теорія Ивасавы, а також інші методи XX століття, які не були доступні П’єру Ферма.
Дві статті, що містять докази, складають 129 сторінок, які писалися протягом семи років. Джон Коутс описав це відкриття як одне з найбільших досягнень теорії чисел, а Джон Конвей назвав його головним математичним звершенням 20 століття. Уайлс, щоб довести останню теорему Ферма шляхом доведення теореми модульності для приватного випадку полустабильных еліптичних кривих, розробив дієві методи підйому модульності і відкрив нові підходи до численних інших проблем. За рішення останньої теореми Ферма він був присвячений в лицарі і отримав інші нагороди. Коли стало відомо, що Уайлс виграв премію Абеля, Норвезька академія наук описала його досягнення як «чудове і елементарне доказ великої теореми Ферма».
Як це було
Одним з людей, що аналізували первісну рукопис Уайлса з рішенням теореми, був Нік Кац. У ході огляду він задав британцеві ряд уточнюючих питань, які змусили Уайлса визнати, що його робота явно містить пробіл. В одній критичній частині докази була допущена помилка, яка давала оцінку для порядку конкретної групи: система Ейлера, яка використовується для розширення методу Колывагина і Флача, була неповною. Помилка, однак, не зробила його роботу марною – кожна частина роботи Уайлса була дуже значною і новаторською сама по собі, як і багато розробок і методи, які він створив в ході своєї роботи і які зачіпали лише одну частину рукопису. Тим не менш, у цій первісної роботі, опублікованій у 1993 році, дійсно не було докази великої теореми Ферма.

Уайлс провів майже рік, намагаючись заново знайти рішення теореми – спершу поодинці, а потім у співпраці зі своїм колишнім учнем Річардом Тейлором, але все, здавалося, було марним. До кінця 1993 року поширилися чутки, що при перевірці доказ Уайльса зазнало невдачі, але наскільки серйозною була ця невдача, відомо не було. Математики почали чинити тиск на Уайлса, щоб він розкрив деталі своєї роботи, незалежно від того, була вона виконана чи ні, щоб більш широке співтовариство математиків могло досліджувати і використовувати все, чого йому вдалося домогтися. Замість того, щоб швидко виправити свою помилку, Уайлс лише виявив додаткові складні аспекти доведення великої теореми Ферма, і нарешті усвідомив, наскільки складною вона є.
Уайлс заявляє, що вранці 19 вересня 1994 року він був на межі того, щоб кинути все і здатися, і майже змирився з тим, що зазнав невдачі. Він готовий був видати свою незакінчену роботу, щоб інші могли на ній грунтуватися і знайти, у чому він помилився. Англійський математик вирішив дати собі останній шанс і в останній раз проаналізував теорему, щоб спробувати зрозуміти основні причини, за якими його підхід не працював, як раптом усвідомив, що підхід Колывагина-Флак не буде працювати, поки він не залучить до процесу докази ще й теорію Ивасавы, змусивши її працювати.
6 жовтня Уайлс попросив трьох колег (включаючи Фалтинса) розглянути його нову роботу, а 24 жовтня 1994 р. він представив дві рукописи – «Модульні еліптичні криві і остання теорема Ферма» і «Теоретичні властивості кільця деяких Гекке-алгебр», другу з яких Уайлс написав спільно з Тейлором і довів, що були виконані певні умови, необхідні для виправдання виправленого кроку в основній статті.
Ці дві статті були перевірені і, нарешті, опубліковані як повнотекстового видання в журналі «Аннали математики» за травень 1995 року. Нові розрахунки Ендрю були широко проаналізовано і наукове співтовариство в кінці кінців їх визнала. У цих роботах була встановлена теорема модульності для полустабильных еліптичних кривих – останній крок до доведення великої теореми Ферма, через 358 років після того, як вона була створена.
Історія великої проблеми
Рішення цієї теореми вважалося найбільшою проблемою в математиці протягом багатьох століть. У 1816 і 1850 роках Французька академія наук запропонувала приз за загальне доказ великої теореми Ферма. У 1857 році Академія присудила 3000 франків і золоту медаль Куммеру за дослідження ідеальних чисел, хоча він і не подавав заявку на приз. Ще одна премія йому була запропонована в 1883 році Брюссельської академією.
Премія Вольфскеля
У 1908 році німецький промисловець і математик-аматор Пауль Вольфскель заповів 100 000 золотих марок (велику суму для того часу) Академії наук Геттінгена, щоб ці гроші стали призом за повний доказ великої теореми Ферма. 27 червня 1908 року Академія опублікувала дев’ять правил нагородження. Серед іншого, ці правила вимагали опублікування докази в рецензованому журналі. Приз мав присуджуватися лише через два роки після публікації. Термін конкурсу повинен був закінчитися 13 вересня 2007 – приблизно через століття після свого початку. 27 червня 1997 року Уайлс отримав призові гроші Вольфсхеля, а потім ще 50 000 доларів. В березні 2016 року він отримав 600 000 євро від уряду Норвегії в рамках премії Абеля за «приголомшливе доказ великої теореми Ферма за допомогою гіпотези модульності для полустабильных еліптичних кривих, що відкриває нову еру в теорії чисел». Це був світовий тріумф скромного англійця.

До докази Уайлса теорема Ферма, як вже говорилося раніше, вважалася абсолютно нерозв’язної протягом цілих століть. Тисячі невірних доказів у різний час були представлені комітету Вольфскеля, склавши приблизно 10 футів (3 метри) кореспонденції. Тільки в перший рік існування премії (1907-1908) було подано 621 заявок з претензією на рішення теореми, хоча до 1970-м років їх кількість зменшилася приблизно до 3-4 заявок на місяць. На думку Ф. Шлихтинга, рецензента Вольфсхеля, більшість доказів були засновані на елементарних методи, що викладаються в школах, і часто представлялися «людьми з технічною освітою, але невдалої кар’єрою». За словами історика математики Говарда Эйвса, остання теорема Ферма встановила своєрідний рекорд – це теорема, яка набрала найбільшу кількість хибних доказів.
Лаври Ферма японцям дісталися
Як вже говорилося раніше, приблизно в 1955 році японські математики Горо Шімури і Ютака Таніяма відкрили можливий зв’язок між двома, мабуть, зовсім різними галузями математики – еліптичними кривими і модульними формами. Отримана в результаті їх досліджень теорема модульності (в той час відома як гіпотеза Таниямы-Шимуры) свідчить, що кожна еліптична крива є модулярної, що означає, що вона може бути пов’язана з унікальною модулярної формою.
Теорія спочатку була відхилена як малоймовірна або досить спекулятивна, але була сприйнята більш серйозно, коли теоретик чисел Андре Вейль знайшов докази, що підтверджують висновки японців. В результаті гіпотеза часто називалася гіпотезою Таниямы-Шимуры-Вейля. Вона стала частиною програми Langlands, що представляє собою список важливих гіпотез, що вимагають докази в майбутньому.
Навіть після серйозної уваги, гіпотеза була визнана сучасними математиками як надзвичайно важка або, можливо, недоступна для доказу. Тепер саме ця теорема чекає свого Ендрю Уайлса, який зміг би здивувати весь світ її рішенням.

Теорема Ферма: доказ Перельмана
Не дивлячись на розхожий міф, російський математик Григорій Перельман, при всій своїй геніальності, не має ніякого відношення до теоремі Ферма. Що, втім, ніяк не применшує його численних заслуг перед науковим співтовариством.

