Піраміда – це просторовий полиэдр, або многогранник, який зустрічається в геометричних задачах. Основними властивостями цієї фігури є її об’єм і площа поверхні, які обчислюються із знання будь-яких двох її лінійних характеристик. Однією з таких характеристик є апофема піраміди. Про неї піде мова в статті.
Фігура піраміда
Перш ніж наводити визначення апофемы піраміди, познайомимося з самою фігурою. Піраміда являє собою багатогранник, який утворений одним n-вугільним підставою і n трикутниками, складовими бічну поверхню фігури.
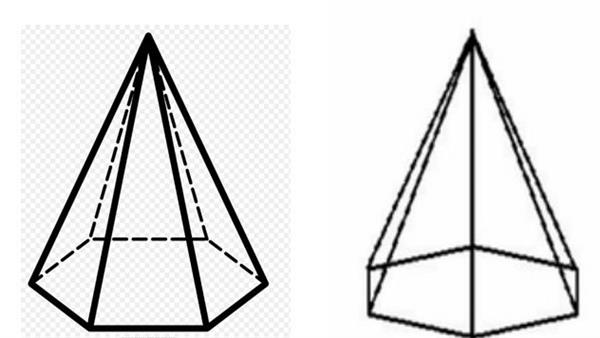
Кожна піраміда має вершину – точку з’єднання всіх трикутників. Перпендикуляр, проведений із цієї вершини до основи, називається висотою. Якщо висота перетинає в геометричному центрі підстава, то фігура називається прямою. Піраміда пряма, що має равностороннее основа, називається правильною. На малюнку показана піраміда з шестикутним підставою, на яку дивляться з боку грані і ребра.
Апофема правильної піраміди
Її також називають апотемой. Під нею розуміють перпендикуляр, проведений з вершини піраміди на стороні підстави фігури. За своїм визначенням цей перпендикуляр відповідає висоті трикутника, який утворює бічну грань піраміди.
Оскільки ми розглядаємо правильну піраміду з n-вугільним підставою, то всі n апофем для неї будуть однаковими, оскільки такими є рівнобедрені трикутники бічній поверхні фігури. Зауважимо, що однакові апофемы є властивістю правильної піраміди. Для фігури загального типу (похилій з неправильним n-кутником) всі n апофем будуть різними.
Ще однією властивістю апофемы піраміди правильної є те, що вона одночасно є висотою, медіаною і бісектрисою відповідного трикутника. Це означає, що вона ділить його на два однакових прямокутних трикутника.
Трикутна піраміда і формули для визначення її апофемы
У будь правильній піраміді важливими лінійними характеристиками є довжина сторони її основи, бічне ребро b, висота h і апофема hb. Ці величини один з одним пов’язані відповідними формулами, які можна отримати, якщо накреслити піраміду і розглянути необхідні прямокутні трикутники.
Правильна трикутна піраміда складається з 4 трикутних граней, причому одна з них (підстава) має бути обов’язково рівносторонньою. Решта є равнобедренными в загальному випадку. Апофему трикутної піраміди можна визначити через інші величини за такими формулами:
hb = √(b2 – a2/4);
hb = √(a2/12 + h2)
Перше з цих виразів справедливо для піраміди з будь-яким правильним підставою. Другий вираз характерно виключно для трикутної піраміди. Воно показує, що апофема завжди більше висоти фігури.
Не слід плутати апофему піраміди з такою для багатогранника. В останньому випадку апофемой називається перпендикулярний відрізок, проведений на стороні багатогранника з його центру. Наприклад, апофема рівностороннього трикутника дорівнює √3/6*a.
Завдання на обчислення апофемы
Нехай дана правильна піраміда з трикутником в підставі. Необхідно обчислити її апофему, якщо відомо, що площа трикутника дорівнює 34 см2, а сама піраміда складається з 4 однакових граней.
У відповідності з умовою задачі ми маємо справу з тетраедром, що складається з рівносторонніх трикутників. Формула площі для однієї грані має вигляд:
S = √3/4*a2
Звідки отримуємо довжину сторони a:
a = 2*√(S/√3)
Для визначення апофемы hb скористаємося формулою, що містить бічне ребро b. У розглянутому випадку його довжина дорівнює довжині підстави, маємо:
hb = √(b2 – a2/4) = √3/2*a
Підставляючи значення a через S, отримаємо кінцеву формулу:
hb = √3/2*2*√(S/√3) = √(S*√3)
Ми отримали просту формулу, в якій апофема піраміди залежить тільки від площі її основи. Якщо підставити значення S з умови задачі, то отримаємо відповідь: hb ≈ 7,674 див.
