Коли людина чує слово “піраміда”, то відразу згадує величні єгипетські споруди. Тим не менш древні кам’яні гіганти є лише одним з представників класу пірамід. У цій статті розглянемо з геометричної точки зору властивості правильної чотирикутної піраміди .
Що таке піраміда в загальному випадку?
В геометрії під нею розуміють об’ємну фігуру, отримати яку можна, якщо з’єднати всі вершини плоского багатокутника з однією єдиною точкою, що лежить в іншій площині, ніж цей багатокутник. Малюнок нижче показує 4 фігури, які задовольняють даного визначення.
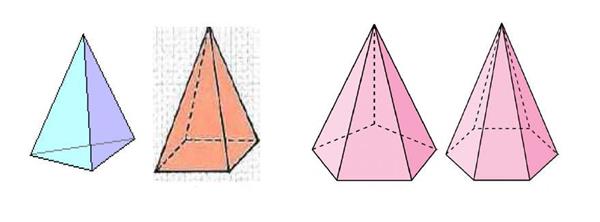
Ми бачимо що перша фігура має трикутний основа, друга – чотирикутний. Дві останні представлені п’яти – і шестикутним підставою. Однак бічна поверхня всіх пірамід утворена трикутниками. Їх кількість точно дорівнює кількості сторін або вершин багатокутника в підставі.
Особливим типом пірамід, які від інших представниць класу відрізняються ідеальною симетрією, є правильні піраміди. Щоб фігура була правильною, повинні виконуватися наступні дві обов’язкові умови:
- в основі повинен знаходитися правильний багатокутник;
- бічна поверхня фігури повинна складатися з рівних рівнобедрених трикутників.
Зазначимо, що друга обов’язкова умова можна замінити іншим: перпендикуляр, проведений з вершини до основи піраміди (точка перетину бічних трикутників), повинен перетинати цю підставу в його геометричному центрі.

