Математика і фізика є, мабуть, двома науковими дисциплінами, які найближче пов’язані один з одним. Так, результати одного з них використовуються для розвитку іншого. Одним з яскравих прикладів, що відображають їх взаємодію, є розрахунок моменту інерції прямокутника відносно осі.
Про момент інерції математики та фізики
Багато люди, знайомі з фізикою чи математикою, напевно, чули про це поняття. Тим не менш, варто розібратися в ньому докладніше, щоб не виникало плутанини.
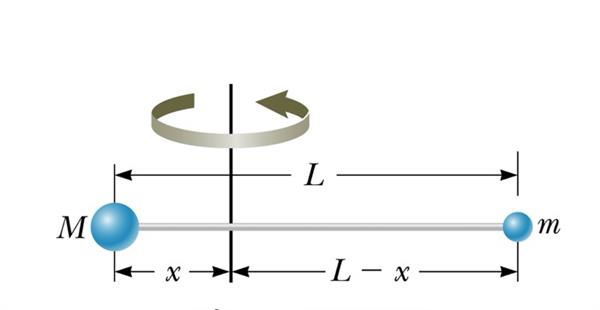
У фізиці під моментом інерції розуміють характеристику обертової системи, яка описує інерційні властивості тіла. Наприклад, для точки з масою m, яка здійснює кругові рухи навколо осі, що знаходиться від неї на відстані r, ця величина виражається формулою:
I = m*r2.
Звідки видно, що описується вона кілограмами на квадратний метр.
В математиці момент інерції – це зовсім інша річ, яка обчислюється не щодо тривимірного об’єкта, а щодо плоского тіла або перетину. У загальному випадку можна говорити про момент інерції n-го порядку. У даній же статті, при обчисленні моменту інерції прямокутника, мова піде про величину другого порядку.
Момент інерції 2-го порядку для перерізу
Варто перейти до математичного формулювання розглянутої величини. Отже, в математиці вона з’являється у вигляді наступного визначення:
Io = ∫∫A(r2*dA).
Тут Io – момент інерції другого порядку, обчислюваний відносно осі O; A – площа сектора, для якого визначається величина Io; dA – елемент площі сектора, який знаходиться від осі O на відстані r.
Ця формула показує, що розмірністю Io є одиниця відстані в четвертому ступені (м4), що відрізняє його від моменту інерції тіла у фізиці (див. пункт вище).
Навіщо обчислюють величину Io? Звичайно ж, це не чиста математична задача, яка не має прикладного характеру. Момент інерції Io для перерізів різної форми необхідний при розрахунках згинальних напружень в інженерних конструкціях, наприклад, для балок.
Далі наведено розрахунки для осьового моменту інерції прямокутника при різному положенні осі обертання O щодо об’єкта.
Вісь проходить через центр фігури паралельно одній із сторін
Нехай дано прямокутник з розмірами сторін a і b. Припустимо, що вісь O ділить фігуру на дві рівні половини і паралельна стороні a. Ця ситуація зображена на малюнку нижче.
Подвійний інтеграл для такої ситуації можна порахувати досить просто, оскільки відстань r будь-якого елемента з площею dA буде дорівнює x. При цьому інтегрування проводиться від -b/2 до +b/2 (вісь O перетинає початок координат по осі x). Що стосується меж інтегрування по y, то їх можна вибрати, як від -a/2 до +a/2 (початок координат у центрі фігури), так і від 0 до a (початок координат лежить на середині однієї з сторін довжиною b). Для визначеності варто вибрати другий варіант. Тоді загальна формула для моменту інерції другого порядку запишеться у вигляді:
Io = ∫0a∫-b/2+b/2(x2*dx*dy).
Обчислюємо подвійний інтеграл по порядку, підставляємо відомі межі, виходить:
Io = x3/3|-b/2+b/2*y|0a = b3*a/12.
Таким чином, отримана формула моменту інерції прямокутника для осі, що проходить через його середину паралельно сторонам з довжиною a.
Очевидно, що якщо вісь буде проходити паралельно сторонам b, то нічого не зміниться в розрахунку, за винятком того, що позначення сторін поміняються місцями. Тобто вийде формула:
Io = a3*b/12.
Вісь проходить через сторону прямокутника
В цьому випадку ситуація повністю аналогічна до попередньої, тільки тепер вісь O1 зміщена до одного з країв фігури. Для розрахунку такого моменту інерції необхідно лише змінити межі інтегрування по відповідній стороні.
Нехай вісь O1 буде проходити через сторону a, тоді межі інтегрування по x від 0 до b. Якщо підставити їх у формулу, отримаємо:
Io1 = x3/3|0b*y|0a = b3*a/3.
Відповідно, якщо вісь O1 проходить через b, тоді вийде:
Io1 = a3*b/3.
Як видно, зсув осі до краю фігури призводить до збільшення її моменту інерції в 4 рази.
Варто зазначити, що формули для випадку, розглянутого в даному пункті, можна було отримати з використанням теореми Штейнера, яка має аналогічний вигляд, що і у випадку розрахунку моменту інерції тіла у фізиці:
Io1 = Io + d2*A.
Тут d – відстань між осями O O1. Якщо обидві осі паралельні сторонам a фігури, тоді d = b/2 (половина довжини сторони b прямокутника). Оскільки площа прямокутника дорівнює a*b, то вийде:
Io1 = b3*a/3 + (b/2)2*a*b = b3*a/12 + b3*a/4 = b3*a/3.
Таким же чином застосовується ця теорема для осі O1, паралельної стороні b, тільки d в цьому випадку буде дорівнює уже a/2.
